luffy博客

树(Tree)

11/9/2023 data-structure

# “树”数据结构详解

树是一种重要的非线性数据结构，它模拟了层次化的数据集，广泛应用于计算机科学中的多个领域。在这篇文档中，我们将深入探讨树的不同类型及其应用。

# 基础概念

  • 节点（Node）: 树的基本单位，包含数据和链接到其他节点的链接。
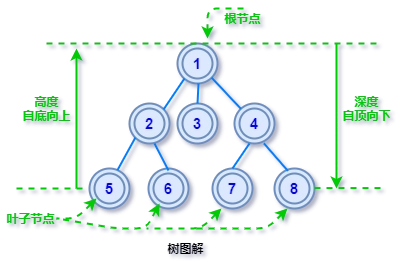
  • 根节点（Root）: 没有父节点的顶层节点。
  • 子节点（Child）: 一个节点的直接下级节点。
  • 父节点（Parent）: 一个节点的直接上级节点。
  • 叶节点（Leaf）: 没有子节点的节点。
  • 深度（Depth）: 从根节点到一个节点的路径长度。
  • 高度（Height）: 从一个节点到最远叶节点的最长路径长度。
  • 子树（Subtree）: 任意节点及其所有后代构成的树。

# 树的类型

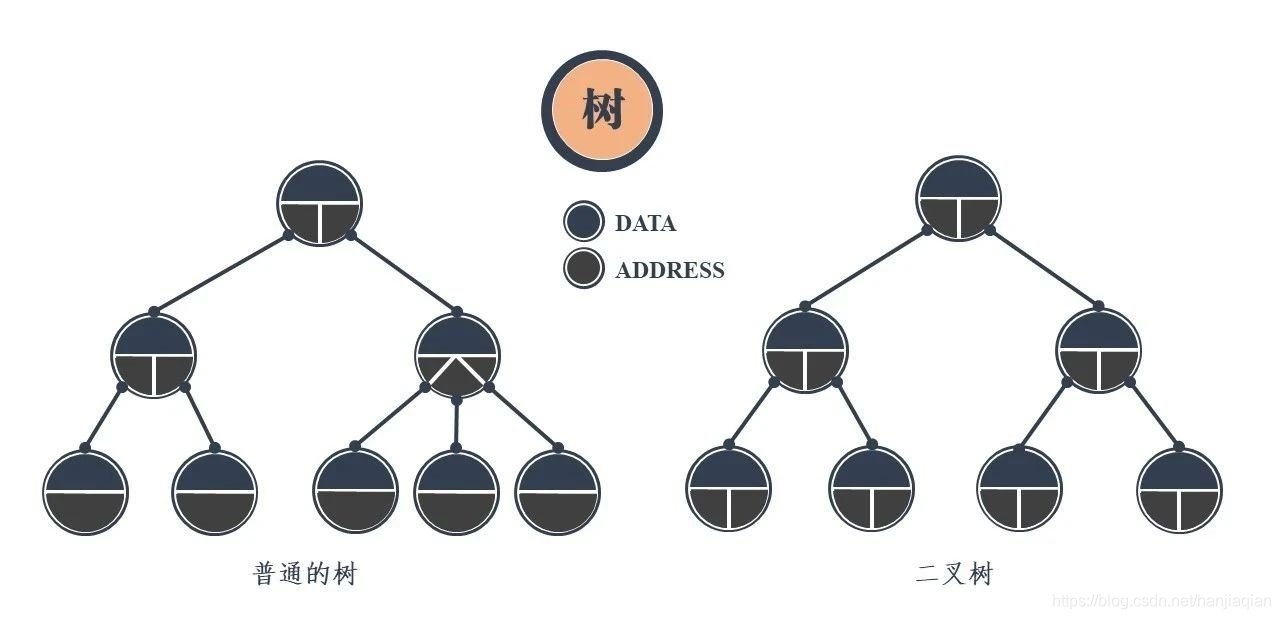
# 1. 二叉树（Binary Tree）

  • 定义: 每个节点最多有两个子节点的树。
  • 应用: 实现二叉搜索树、堆结构、语法树。

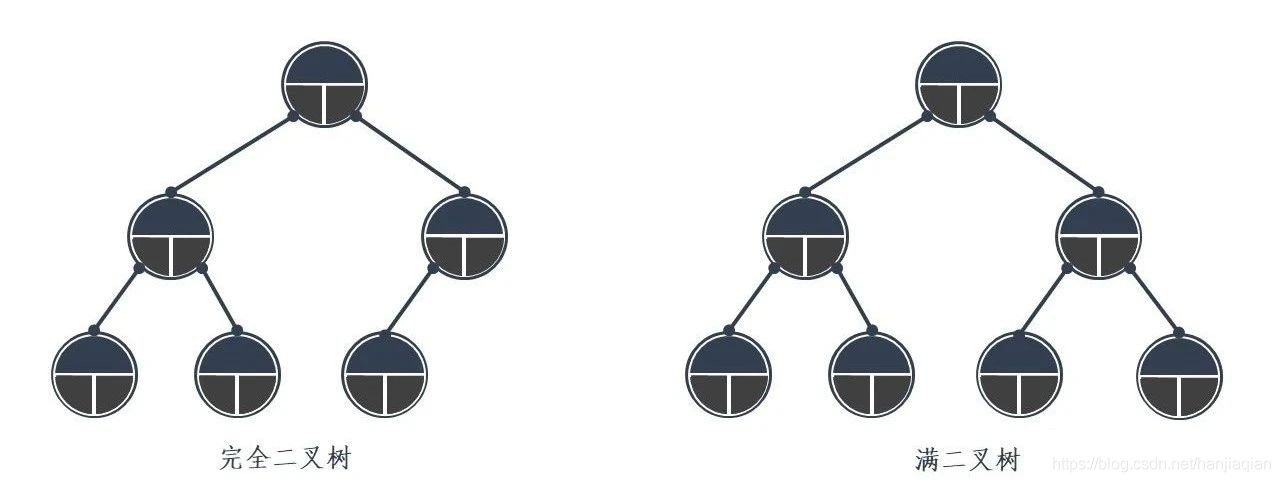
# 2.完全二叉树 、 满二叉树

完全二叉树：除了最后一层结点，其它层的结点数都达到了最大值；同时最后一层的结点都是按照从左到右依次排布。

满二叉树:除了最后一层，其它层的结点都有两个子结点。

# 3.平衡二叉树

平衡二叉树又被称为AVL树，它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

# 4.红黑树

1.根结点为黑色
2.每一个节点不是黑色就是红色
3.每个叶子结点是黑色的。
4.如果一个结点是红色的，那么子节点必须为黑色。
5.从一个节点到该节点的叶子节点的所有路径上包含相同数目的黑节点。

# 二叉树的性质

俗话说：性质学得好，弯路少走一半！

# 1.层节数

在二叉树的第i层上最多有2^{i-1}个结点(i>=1)

# 2.总结点

深度为k的二叉树最多有2^{k}-1个结点(k>=1)

# 3.深度

对于任意一棵二叉树，度为0的结点数等于度为2的结点数+1。

# 4.结点数

对于任意一棵二叉树，度为0的结点数等于度为2的结点数+1。

# 5.孩子节点

结点为i双亲结点为i/2向下取整，左孩子2i，右孩子2i+1

上面的性质我就不推导了，其实就是实在不想写了。

# 二叉树遍历

# 1.先序遍历

遍历顺序：根结点->左子树->右子树

void  PreOrder(BiTree root) 
/*先序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
{
 if (root!=NULL)
 {
  Visit(root ->data);  /*访问根结点*/
  PreOrder(root ->LChild);  /*先序遍历左子树*/
  PreOrder(root ->RChild);  /*先序遍历右子树*/
 }
}
1
2
3
4
5
6
7
8
9
10

# 2.中序遍历

遍历顺序：左子树->根结点->右子树

void  InOrder(BiTree root)  
/*中序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
{
 if (root!=NULL)
 {
  InOrder(root ->LChild);   /*中序遍历左子树*/
  Visit(root ->data);        /*访问根结点*/
  InOrder(root ->RChild);   /*中序遍历右子树*/
 }
}
1
2
3
4
5
6
7
8
9
10

# 3.后序遍历

遍历顺序：左子树->右子树->根结点

void  PostOrder(BiTree root)  
/*后序遍历二叉树, root为指向二叉树(或某一子树)根结点的指针*/
{
 if (root!=NULL)
 {
  PostOrder(root ->LChild);   /*后序遍历左子树*/
  PostOrder(root ->RChild);   /*后序遍历右子树*/
     Visit(root ->data);        /*访问根结点*/
     }
}
1
2
3
4
5
6
7
8
9
10

# 4.层次遍历

算法讲解 就是一层一层的从左至右输出，算法不要求掌握

# 遍历算法的简单应用

# 1.建立二叉链表存储的二叉树

void CreateBiTree(BiTree *bt)
   //按“扩展先序遍历序列”建立二叉树的二叉链表的算法
{
    char ch;
    ch = getchar();
    if(ch=='.') *bt=NULL;  // 输入时以点号“. ”表示空结点。
    else 
    {
        *bt=(BiTree)malloc(sizeof(BiTNode)); //生成一个新结点  
        (*bt)->data=ch;
        CreateBiTree(&((*bt)->LChild)); //生成左子树
        CreateBiTree(&((*bt)->RChild)); //生成右子树
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 2.输出叶子结点

void  PreOrder(BiTree root) 
/*先序遍历二叉树, root为指向二叉树根结点的指针*/
{
 if (root!=NULL)
 {
  if (root ->LChild==NULL && root ->RChild==NULL)
   printf("%c  ",root ->data);  /*输出叶子结点*/
  PreOrder(root ->LChild);  /*先序遍历左子树*/
  PreOrder(root ->RChild);  /*先序遍历右子树*/
 }
}
1
2
3
4
5
6
7
8
9
10
11
12

# 3.统计二叉树叶子结点数目

/* LeafCount保存叶子结点的数目的全局变量,调用之前初始化值为0 */ 
方法一：
void leaf_a(BiTree root)
{
 if(root!=NULL)
 {
  leaf_a(root->LChild); 
            leaf_a(root->RChild);
  if (root ->LChild==NULL && root ->RChild==NULL)
   LeafCount++;
 }
}
1
2
3
4
5
6
7
8
9
10
11
12

# 4.求二叉树高度

int PostTreeDepth(BiTree bt)   /* 后序遍历求二叉树的高度递归算法 */
{
 int hl,hr,max;
 if(bt!=NULL)
 {
  hl=PostTreeDepth(bt->LChild);  /* 求左子树的深度 */
  hr=PostTreeDepth(bt->RChild);  /* 求右子树的深度 */
  max=hl>hr?hl:hr;              /* 得到左、右子树深度较大者*/
  return(max+1);               /* 返回树的深度 */
 }
 else return(0);             /* 如果是空树，则返回0 */
}
1
2
3
4
5
6
7
8
9
10
11
12

# 树和二叉树转换

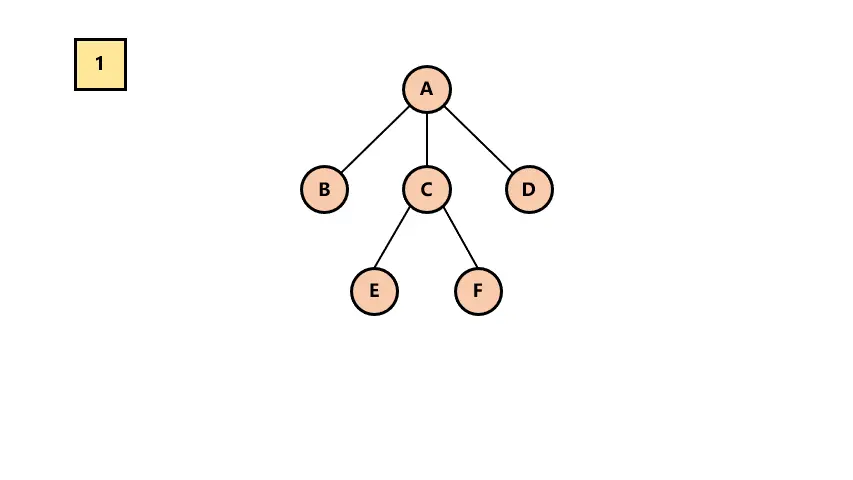
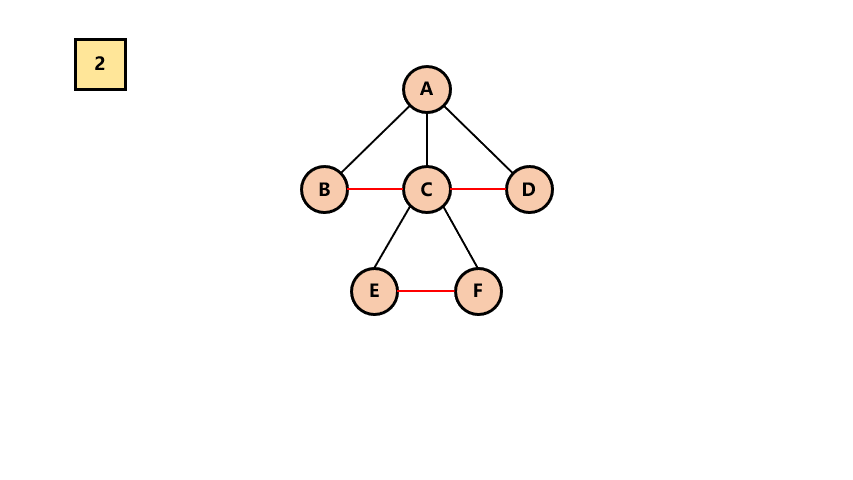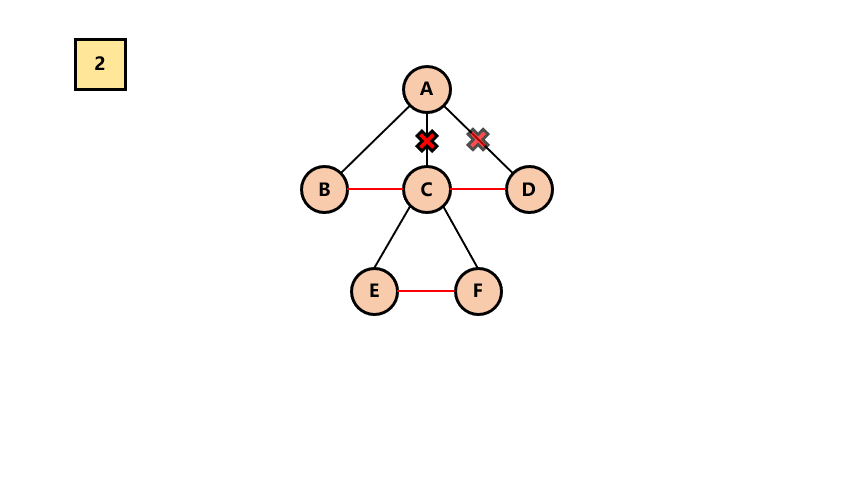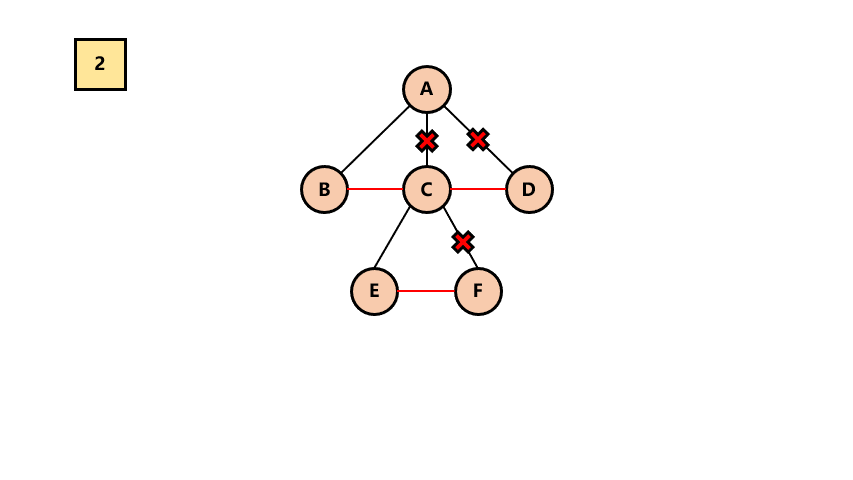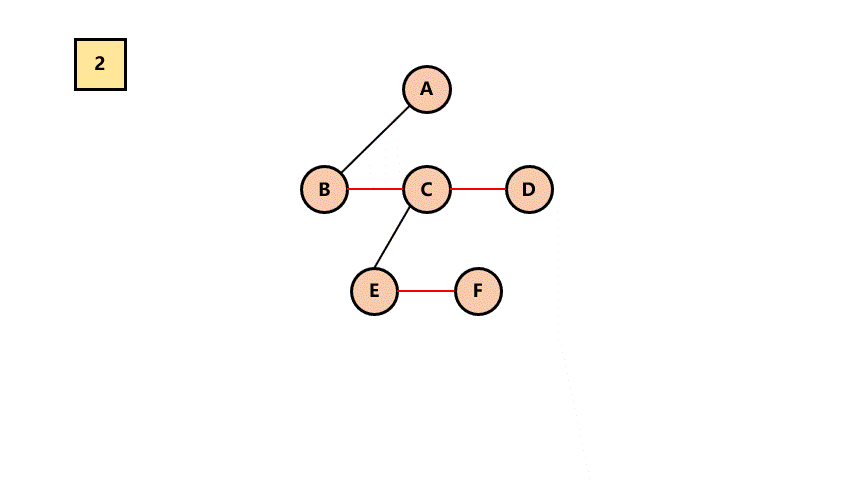
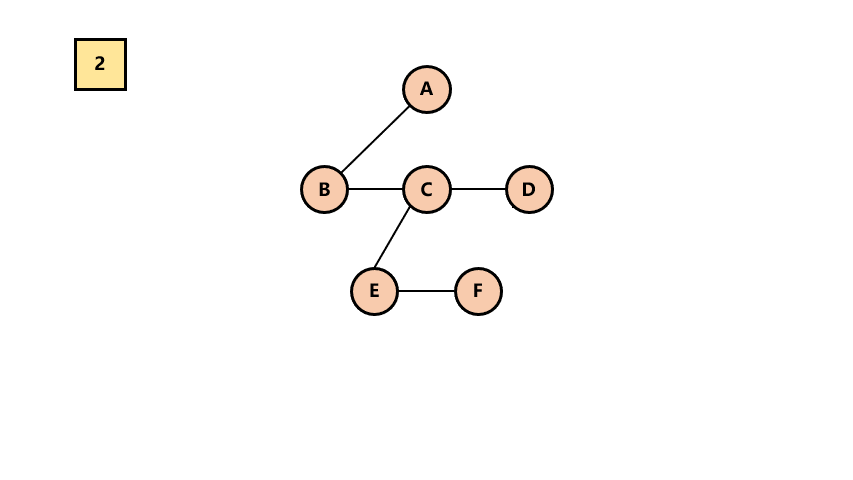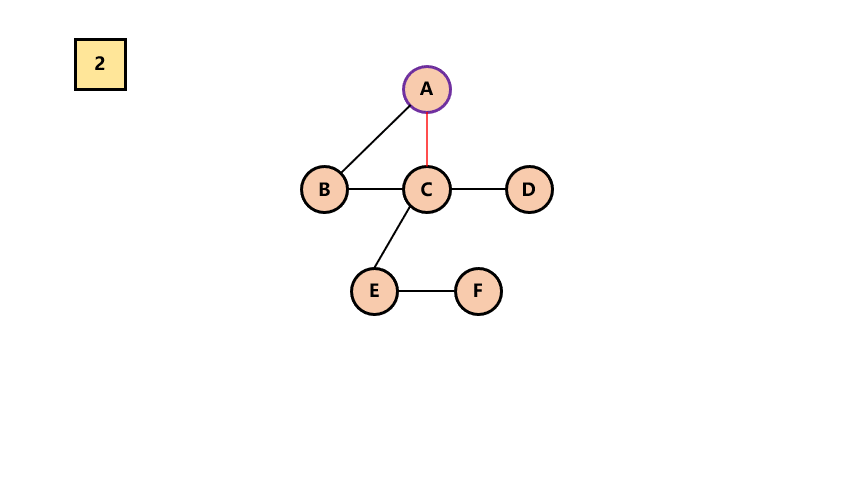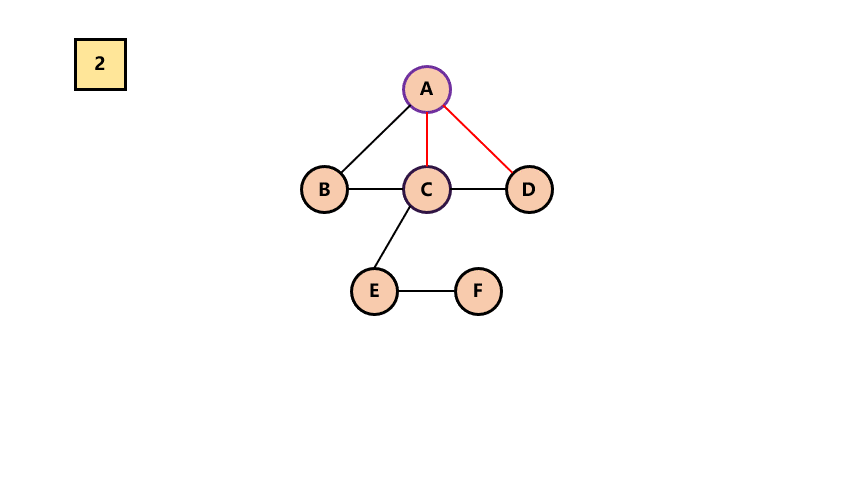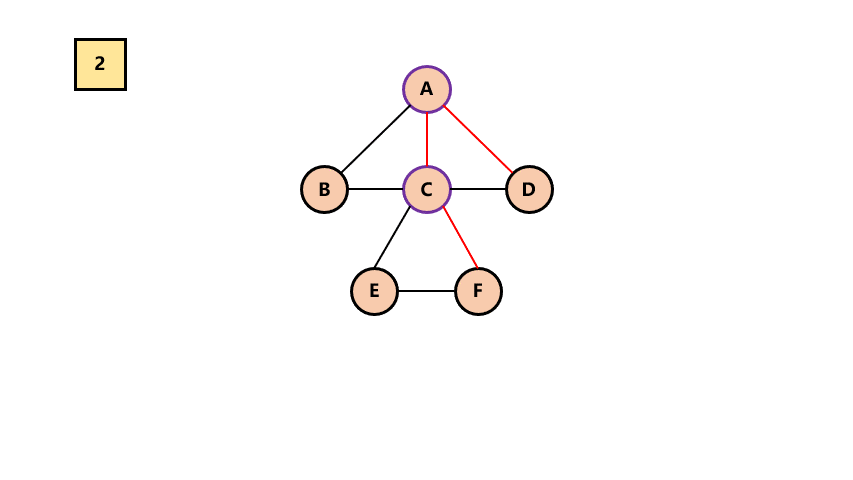
# 1.树 -> 二叉树

连接所有兄弟结点

对树中的每一个结点，只保留与第一个结点的连线，其它删除

整棵树顺时针旋转90度

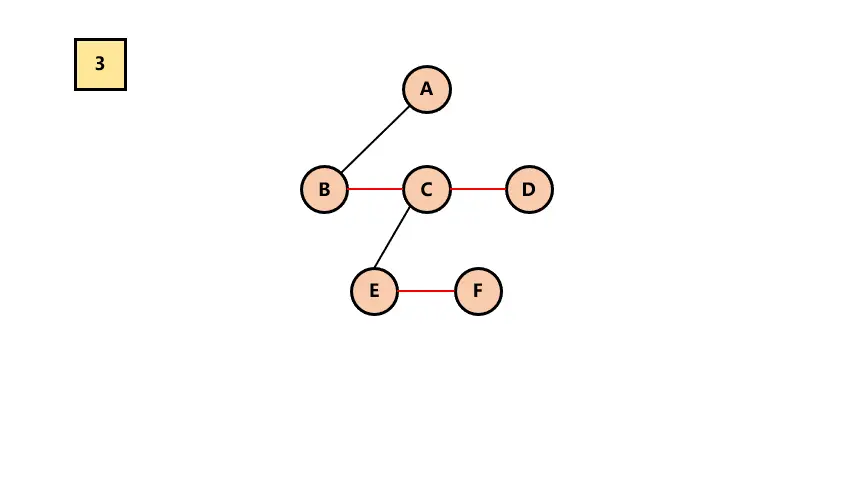
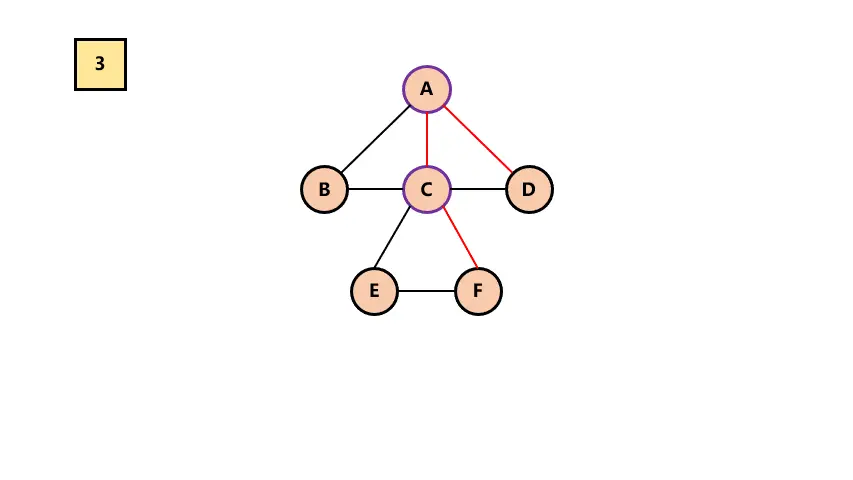
# 2.二叉树 -> 树

将左孩子的右孩子、右孩子的右孩子…全部连接起来

所有双亲结点删除与右孩子的连线

调整一定的角度

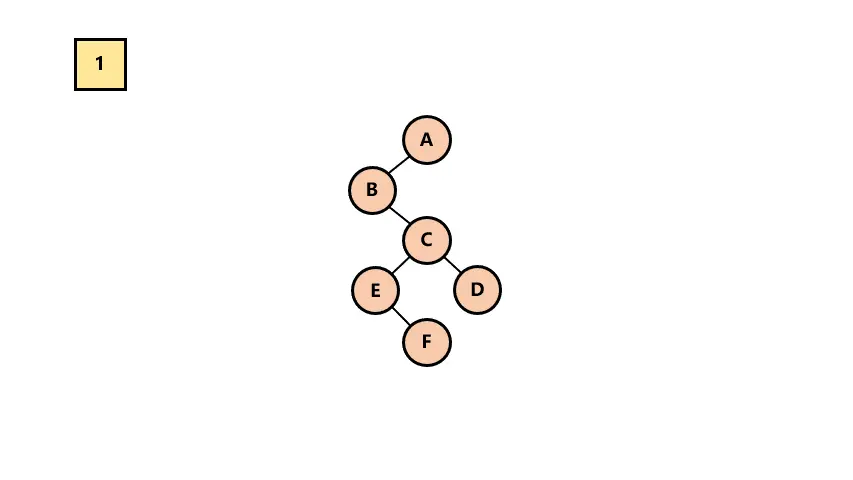
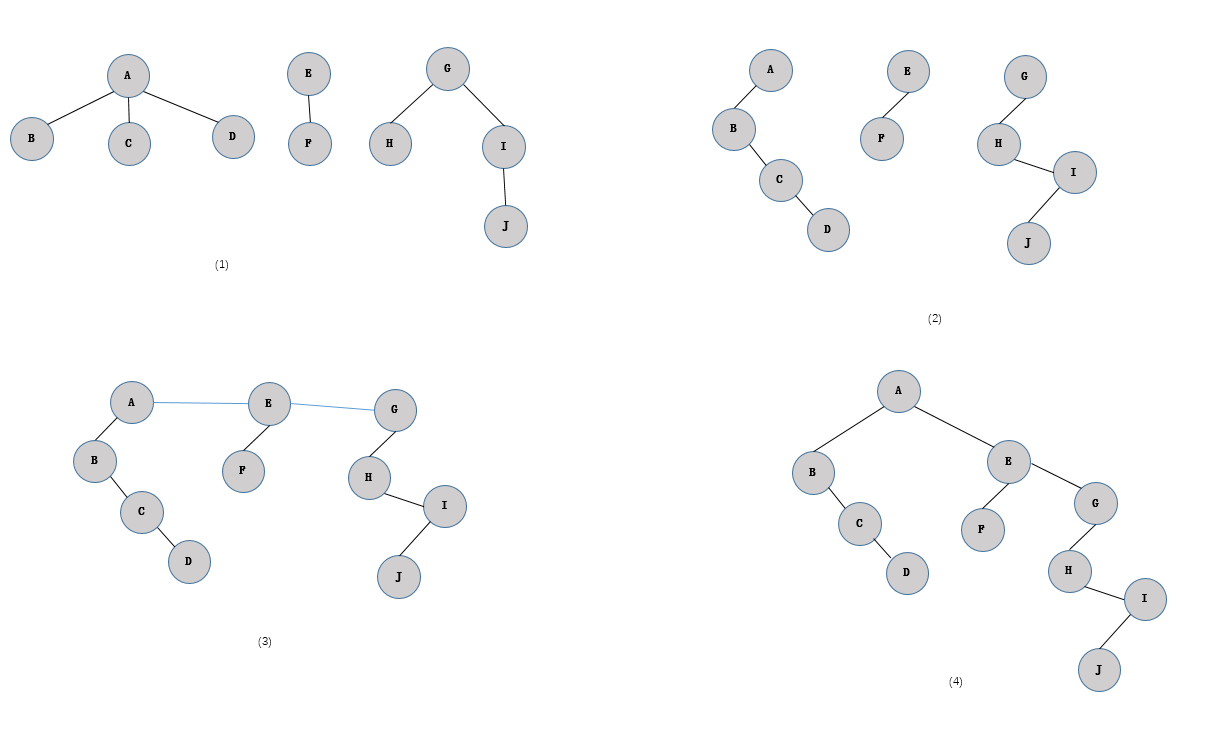
# 3.森林 -> 二叉树

将各棵树分别转换成二叉树

将每棵树的根结点用线相连

以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转，构成二叉树型结构

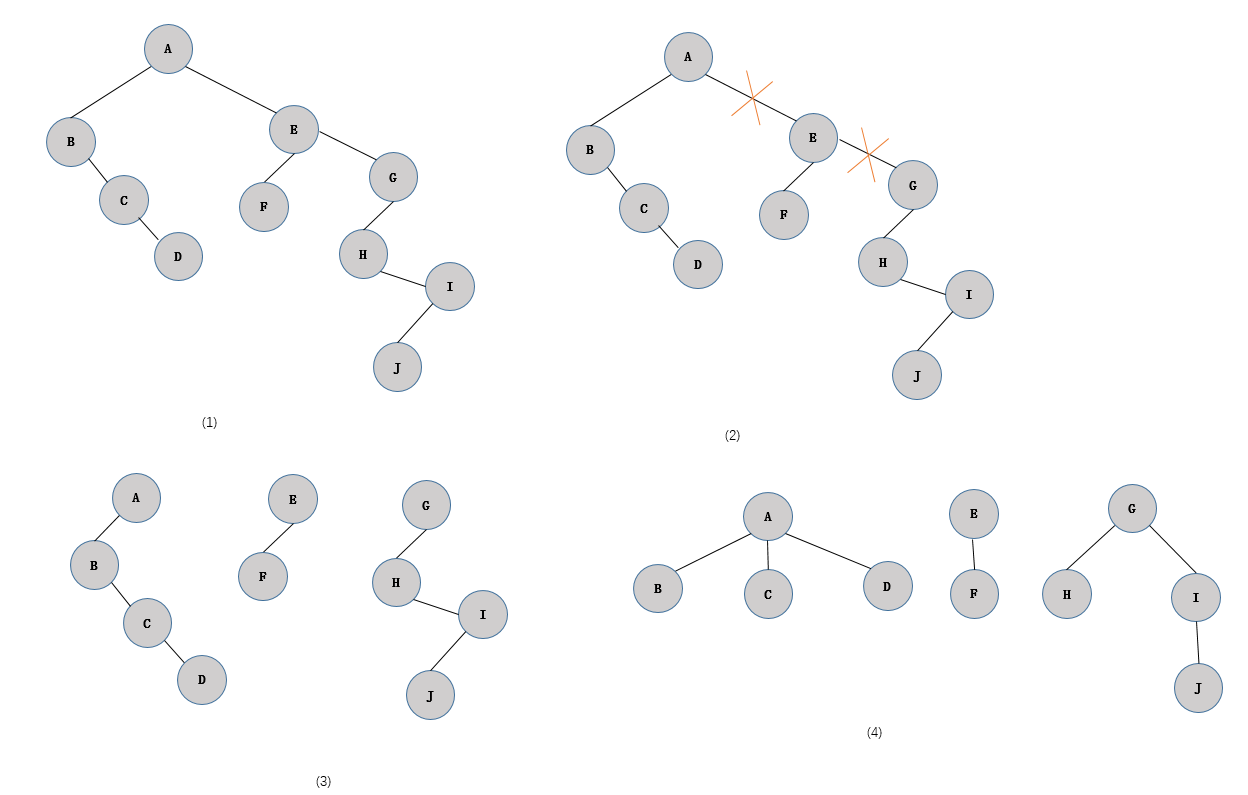
# 4.二叉树 -> 森林

抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉，使之变成孤立的二叉树

还原：将孤立的二叉树还原成树（二叉树→树）

# 二叉树的应用

# 哈夫曼树

# 1.定义

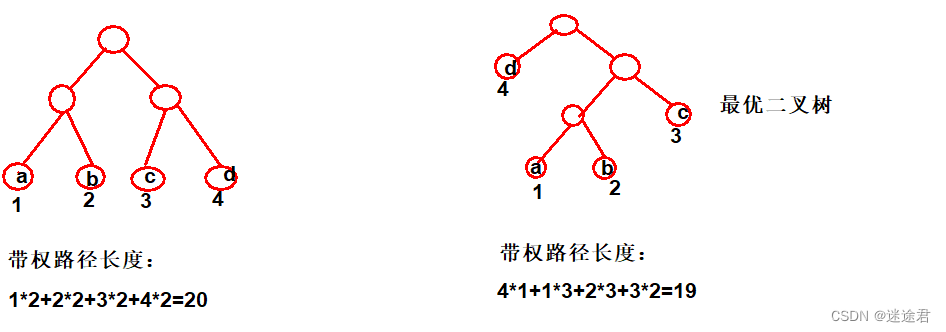
将树中结点赋值，这个值称为这个结点的权值。从树的根到任意结点的路径长度与该节点上权值的乘积，称为该节点的带权路径长度。树中所有叶结点的带权路径长度之和称为该树的带权路径长度。

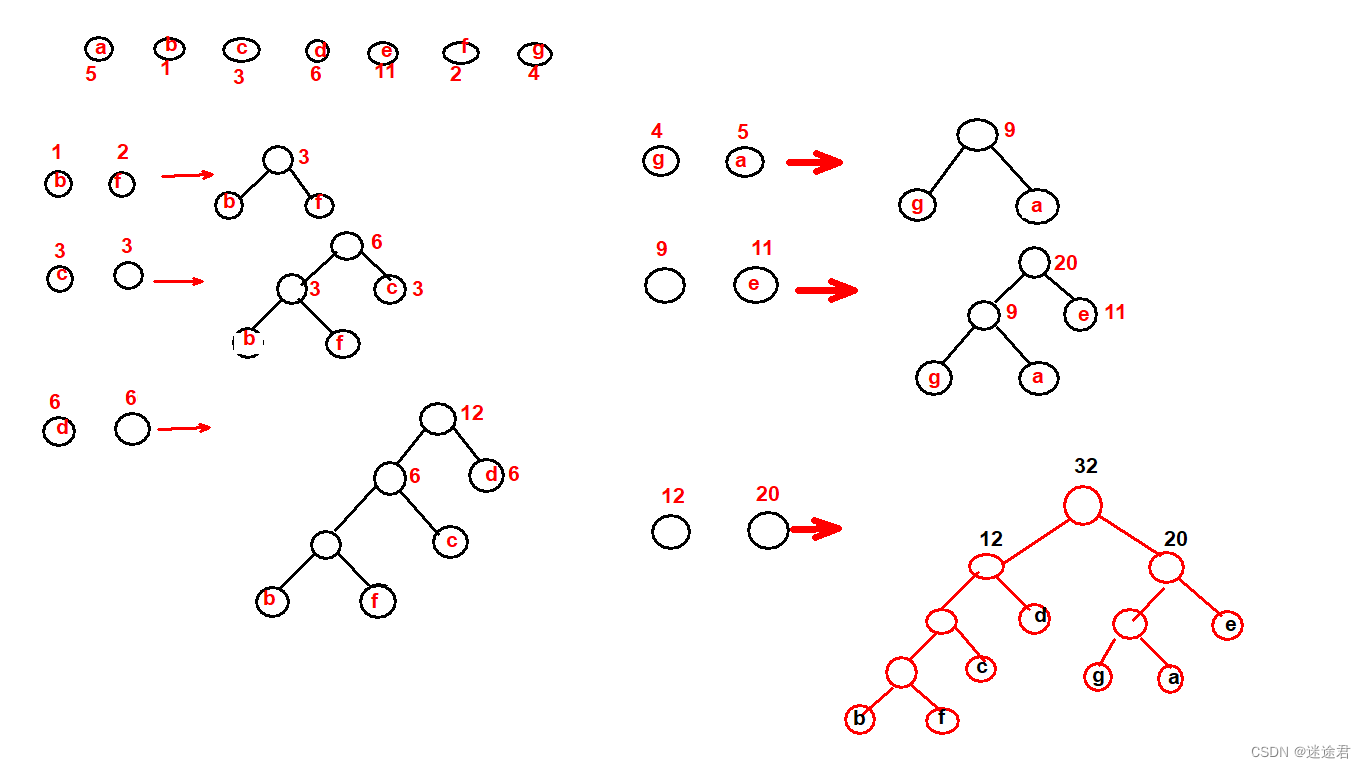
# 2.构造哈夫曼树

1.从结点列表中选出权值第一小和第二小的节点，并组成一棵树，父亲结点的权值等于两结点权值之和。
2.将生成的新树再次放到结点列表之中重复第一步，直到列表中只剩下一个结点

# 3.哈夫曼编码

哈夫曼编码是一种被广泛应用且非常有效的数据压缩编码，将左右子树权值变成0，1，再来进行编码。

Last Updated: 11/30/2023, 2:34:05 PM