数据结构代码题
# 数据结构代码题
# 单链表
单链表的总结:
- 头插法 (头插法放断链)
- 尾插法 (尾插留尾针)
- 逆置法 (头插法实现、全部指针反过来指)
- 归并法 (分解)
- 双指针法 (倒数第 k 个、取较小、中间指针)
- 双循环链表插入删除
# 1.删除 L 单链表中所有值为 x 的结点,并且释放
void Del_x(Linklist L, ElementType x) {
LNode *p = L->next, *pre = L, *q;
// 遍历链表
while (p != NULL) { // Null 改为 NULL
if (p->data == x) { // 找到需要删除的元素
q = p; // 暂存当前节点,准备释放
p = p->next; // 移动到下一个节点
pre->next = p; // 连接前一个节点与下一个节点
free(q); // 释放找到的节点
} else {
pre = p; // 前驱节点前移
p = p->next; // 当前节点前移
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 2.将两个有序顺序表合并为一个新的有序顺序表
bool merge(SqList *A, SqList *B, SqList *C) {
// 检查 C 是否有足够的空间容纳 A 和 B 的所有元素
if (A.length + B.length > C->maxSize) {
return false; // 如果空间不足,返回 false
}
int i = 0, j = 0, k = 0;
// 合并 A 和 B 的元素,按顺序将较小的元素放入 C
while (i < A.length && j < B.length) {
if (A.data[i] < B.data[j]) {
C->data[k++] = A.data[i++]; // A 中的元素较小时,放入 C
} else {
C->data[k++] = B.data[j++]; // B 中的元素较小时,放入 C
}
}
// 如果 A 中还有剩余的元素,继续放入 C
while (i < A.length) {
C->data[k++] = A.data[i++];
}
// 如果 B 中还有剩余的元素,继续放入 C(这里修正为遍历 B)
while (j < B.length) {
C->data[k++] = B.data[j++];
}
return true; // 合并成功
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
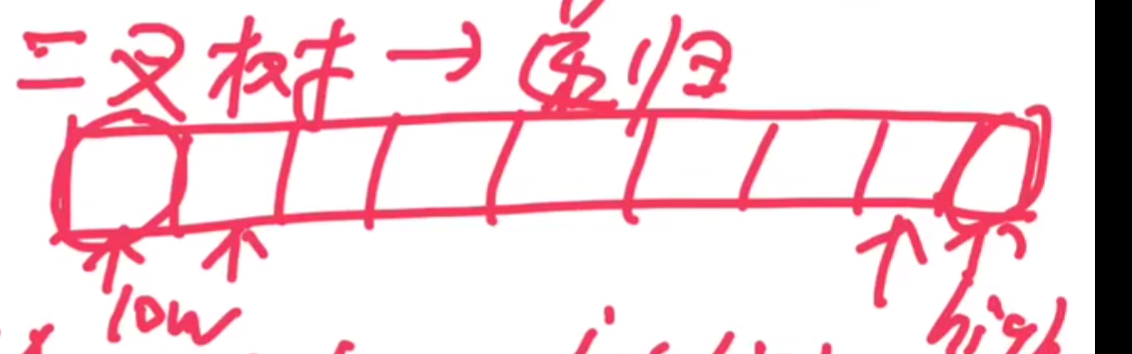
# 3.设计一个高效算法,将顺序表逆置,要求空间复杂度 O(1)
//1、常规法
void reverse(sqList *L){
ElementType temp; //辅助变量
for(int i=0;i<L->length/2;i++){
temp = L->data[i];
L->data[i] = L->data[L->length-i-1];
L->data[L->length-i-1] = temp;
}
}
2
3
4
5
6
7
8
9
10
//2、递归法
void reverse(int *A,int low,int high){
if(low < high){
swap(A[low],A[high]);
reverse(A,low+1,high-1);
}
}
2
3
4
5
6
7
8
# 4.对长度为 n 的顺序表 L,编写一个时间复杂度为 0(n)、空间复杂度为 0(1)的算法,该算法删除线性表中所有值为 x 的数据元素,
void deleteX(SqList *L, ElementType x) {
int i = 0, k = 0; // i 用来遍历顺序表,k 记录要保留的元素位置
// 遍历顺序表 L
while (i < L->length) {
if (L->data[i] != x) {
// 如果当前元素不等于 x,将其保留到前面的空间中
L->data[k++] = L->data[i];
}
i++;
}
// 修改顺序表的长度,去掉所有值为 x 的元素
L->length = k;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 5. 从顺序表中删除其值在给定值 s 与 t 之间(包含 s 和 t,要求 s<t)的所有元素,如果 s 或 t 不合理或顺序表为空,则显示出错信息并退出运行。
bool Dels_t(SqList *L, int s, int t) {
int k = 0; // 记录删除的元素数量
// 如果顺序表为空,或者 s > t,直接返回 false
if (L->length == 0 || s > t) {
return false;
}
for (int i = 0; i < L->length; i++) {
if (L->data[i] >= s && L->data[i] <= t) {
// 如果元素在 [s, t] 范围内,记录删除个数 k
k++;
} else {
// 将不在 [s, t] 范围内的元素前移 k 个位置
L->data[i - k] = L->data[i];
}
}
// 更新顺序表的长度,去掉删除的元素
L->length = L->length - k;
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 6.从有序顺序表中删除所有其值重复的元素,使表中所有元素的值均不同
bool del_same(SqList *L) {
int i = 0, j = 1;
// 如果顺序表为空,直接返回 false
if (L->length == 0) {
return false;
}
// 遍历顺序表,从第二个元素开始
for (; j < L->length; j++) {
// 如果当前元素和前一个不同,保留这个元素
if (L->data[i] != L->data[j]) {
L->data[++i] = L->data[j]; // 将 j 指向的元素前移到 i+1 位置
}
}
// 更新顺序表的长度,i 是最后一个保留元素的下标,因此长度为 i+1
L->length = i + 1;
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 7、己知在一维数组 A[m+n]中依次存放两个线性表(a1,a2,a3..,am)和(b1,b2....,bn)。试编写一个函数,将数组中两个顺序表的位置互换,即将(b1,b2,b3...bn)放在(a1,a2,a3..,am)的前面。
分块逆置 整体逆置
// 逆置数组A中从下标t到下标n的元素
void reverse(int *A, int t, int n) {
int temp;
for (int i = 0; i < (n - t + 1) / 2; i++) { // 逆置范围是 [t, n]
temp = A[t + i];
A[t + i] = A[n - i];
A[n - i] = temp;
}
}
// 将数组中两个线性表的位置互换
void exchange(int *A, int m, int n) {
reverse(A, 0, m - 1); // 逆置前m个元素 (a1, a2, ..., am)
reverse(A, m, m + n - 1); // 逆置后n个元素 (b1, b2, ..., bn)
reverse(A, 0, m + n - 1); // 逆置整个数组
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 8、题目如下

和上面一样三次逆置
# 9、试编写带头节点的的单链表 L 中删除一个最小值节点的高效算法(假设最小值
节点是唯一的)
四个指针,
// 删除单链表L中数据值最小的节点
void deleteMinNode(LinkList L) {
if (L == NULL || L->next == NULL) {
return; // 如果链表为空或只有头节点,直接返回
}
LNode *preMin = L; // 最小值节点的前驱节点
LNode *minNode = L->next; // 最小值节点,初始化为第一个有效节点
LNode *pre = L; // 当前遍历节点的前驱节点
LNode *p = L->next; // 当前遍历节点
// 遍历链表,寻找最小值节点
while (p != NULL) {
if (p->data < minNode->data) {
minNode = p; // 更新最小值节点
preMin = pre; // 更新最小值节点的前驱节点
}
pre = p; // 更新前驱节点
p = p->next; // 移动到下一个节点
}
// 删除最小值节点
preMin->next = minNode->next; // 前驱节点指向最小值节点的下一个节点
free(minNode); // 释放最小值节点的内存
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 10、头插法建立单链表
// 初始化带头节点的单链表,采用头插法插入元素
LinkList initLinkList2() {
LinkList L = (LinkList)malloc(sizeof(LNode)); // 创建头节点
L->next = NULL; // 初始化头节点的 next 指针
LNode *s; // s 是指向新节点的指针
int x;
printf("请输入要插入的元素的值:");
scanf("%d", &x);
// 当输入值不为 -1 时,循环插入元素
while (x != -1) {
s = (LNode *)malloc(sizeof(LNode)); // 分配新节点的内存
s->data = x; // 设置新节点的数据域
s->next = L->next; // 将新节点指向当前头节点后的节点
L->next = s; // 将新节点插入到头节点后面
printf("请输入要插入的元素的值:");
scanf("%d", &x);
}
return L; // 返回带头节点的链表
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 11.尾插法
LinkList initLinkList() {
LinkList L = (LinkList)malloc(sizeof(LNode)); // 创建头节点
L->next = NULL; // 初始化头节点的 next 指针
int x;
printf("请输入要插入的值:");
scanf("%d", &x);
LNode *r = L; // 尾指针,初始化为头节点
while (x != -1) { // -1 表示结束输入
LNode *s = (LNode *)malloc(sizeof(LNode)); // 分配新节点的内存
s->data = x; // 设置新节点的数据
s->next = NULL; // 新节点的 next 置为 NULL
r->next = s; // 尾节点指向新节点
r = s; // 更新尾指针为新节点
printf("请输入要插入的值:");
scanf("%d", &x);
}
return L; // 返回带头节点的链表
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 5 试编写算法将带头节点的单链表就地逆置,所谓的“就地”是指辅助空间的复杂度为 0(1)
//常规逆置(头插法)
LinkList reverse_LinkList(LinkList L) {
LNode *p = L->next; // p指向第一个节点
LNode *r; // 用于保存当前节点的下一个节点
L->next = NULL; // 断开原链表,头节点的next设为NULL
while (p != NULL) {
r = p->next; // 保存p的下一个节点
p->next = L->next; // 将p的next指向已反转部分
L->next = p; // 头节点的next指向p,完成插入
p = r; // 移动到下一个节点
}
return L; // 返回反转后的链表
}
//递归逆置
LinkList reverse(LinkList L){
if(L->next == NULL){
reutnr L;
}
LinkList newhead = reverse(L->next);
L->next->next = L;
L->next = NULL;
reutrn newhead;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 13、设在一个带表头结点的单链表中所有元素的结点的数据值无序,试编写一个函数,删除表中所有介于给定的的两个值(作为函数的参数给出)之间的元素的元素(若存在)
void deletemin_max(LinkList L, int min, int max) {
LNode *p = L->next; // 指向第一个节点
LNode *pre = L; // 指向前一个节点,即头节点
while (p != NULL) {
if (p->data > min && p->data < max) { // 如果当前节点的数据在 (min, max) 范围内
pre->next = p->next; // 删除当前节点
free(p); // 释放当前节点的内存
p = pre->next; // 更新 p 为下一个节点
} else {
pre = p; // 如果不删除当前节点,则更新 pre
p = p->next; // 移动到下一个节点
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 14、给定两个单链表,编写算法找出两个单链表的公共结点。
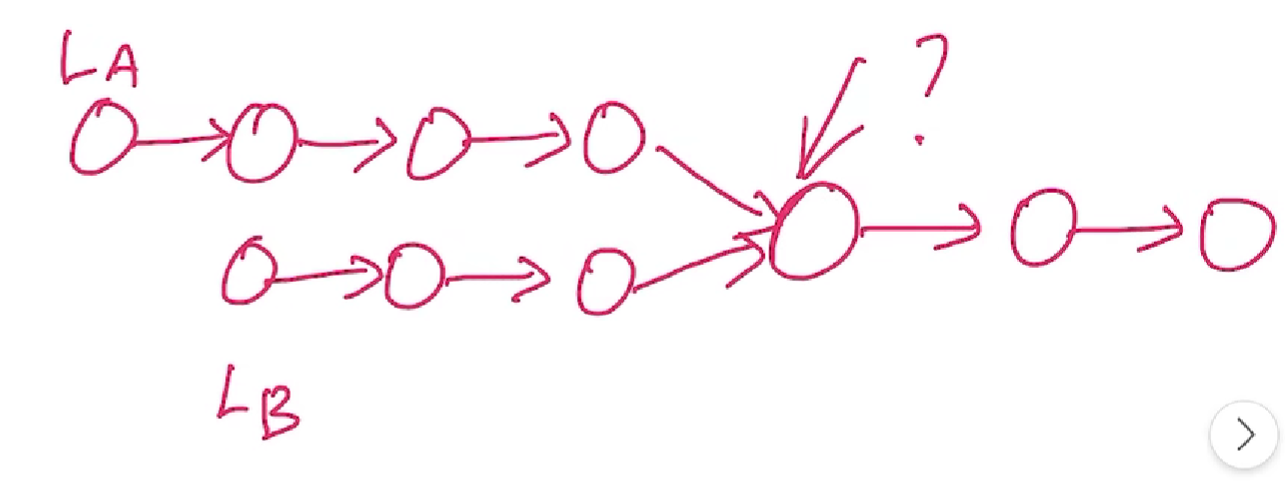
//暴力法
LinkList searchCommon(LinkList A,LinkList B){
LNode *p = A->next,*q;
while(p!=NULL){
q=B->next;
while(q!=NULL){
if(p==q){
return p;
}
q=q->next;
}
p=p->next;
}
}
//优化后
int getLength(LinkList L) {// 计算链表长度
int len = 0;
LNode *p = L->next; // 跳过头节点
while (p != NULL) {
len++;
p = p->next;
}
return len;
}
LinkList searchCommon(LinkList A, LinkList B) {
int lenA = getLength(A); // 获取链表 A 的长度
int lenB = getLength(B); // 获取链表 B 的长度
LNode *p = A->next; // p 指向链表 A 的第一个节点
LNode *q = B->next; // q 指向链表 B 的第一个节点
// 让较长的链表先走几步
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p = p->next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
q = q->next;
}
}
// 同时遍历两个链表,找到公共节点
while (p != NULL && q != NULL) {
if (p == q) { // 找到公共节点
return p;
}
p = p->next;
q = q->next;
}
return NULL; // 如果没有找到公共节点,返回 NULL
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 15.将一个带头结点的单链表 A 分解为两个带头结点的单链表 A 和 B,使得 A 表中含有原表中序号为奇数的元素,而 B 表中含有原表中序号为偶数的元素,且保持其相对顺序不变
void disassemble(LinkList L, LinkList A, LinkList B) {
LNode *p = L->next; // p指向原链表第一个有效节点
LNode *q = A; // q指向A链表的尾部
LNode *r = B; // r指向B链表的尾部
int len = 1; // 用于计数,区分奇偶
while (p != NULL) {
if (len % 2 != 0) { // 奇数位置,插入A链表
q->next = p;
q = p;
} else { // 偶数位置,插入B链表
r->next = p;
r = p;
}
p = p->next; // 更新p,遍历下一个节点
len++; // 计数增加
}
// 确保A和B链表的末尾节点next指向NULL,防止出现循环
q->next = NULL;
r->next = NULL;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 16{a1,b1,a2,b2...an,bn}为线性表,采用带头结点的 hc 单链表存放,设计一个就地算法,将其拆分为两个线性表,使得 A={a1,a2,an},B={bn,.,b2,bl}。
void disassemble(LinkList L, LinkList A, LinkList B) {
LNode *p = L->next; // p指向原链表的第一个有效节点
LNode *t; // 临时指针,用于保存下一个节点
LNode *q = A; // q指向A链表的尾部
LNode *r = B; // r指向B链表的头节点
int len = 1; // 用于计数,区分奇偶
while (p != NULL) {
if (len % 2 != 0) {
// 尾插法插入A
q->next = p;
q = p;
} else {
// 头插法插入B
t = p->next; // 保存下一个节点
p->next = r->next; // 将当前节点插入B的头部
r->next = p; // 更新B链表的头节点
p = t; // 恢复p指向的下一个节点
len++;
continue; // 避免双重更新p
}
len++;
p = p->next;
}
// 确保A和B链表的末尾next指向NULL
q->next = NULL;
r->next = NULL;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 17.在一个递增有序的线性表中,有数值相同的元素存在。若存储方式为单链表,设计算法去掉数值相同的元素,使表中不再有重复的元素,例如(7,10,10,21,30,42,42,42,51,70)将变成(7,10,21,30,42,51,70)
LinkList delete_same(LinkList L) {
if (L->next == NULL || L->next->next == NULL) { // 如果链表为空或只有一个节点,直接返回
return L;
}
LNode *p = L->next->next; // 指向链表的第三个节点
LNode *pre = L->next; // 指向链表的第二个节点(第一个有效节点)
while (p != NULL) {
if (p->data == pre->data) { // 如果当前节点值等于前驱节点值,删除当前节点
pre->next = p->next; // 跳过当前节点
free(p); // 释放当前节点
p = pre->next; // 移动到下一个节点
} else {
pre = p; // 前驱节点移动到当前节点
p = p->next; // 当前节点移动到下一个节点
}
}
return L;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 18、T:假设有两个按元素值递增次序排列的线性表,均以单链表的形式存储。请编写算法将这两个单链表归并为一个按元素值递减次序排列的单链表,并要求利用原本两个单链表的结点存放归并后的单链表。
遍历两个链表,头插法即可
LinkList merge(LinkList A, LinkList B) {
LNode *p = A->next; // A的第一个有效节点
LNode *q = B->next; // B的第一个有效节点
LNode *r; // 用于临时存储节点
A->next = NULL; // 清空A链表的头节点指针,准备头插法 这里很重要,一般不能创建空间都需要这样,前面拿着指针后面置空
// 使用头插法进行倒序合并
while (p != NULL && q != NULL) {
if (p->data < q->data) {
r = p->next; // 暂存下一个节点
p->next = A->next; // 头插法插入到A的前面
A->next = p;
p = r; // 移动到下一个节点
} else {
r = q->next;
q->next = A->next;
A->next = q;
q = r;
}
}
// 合并剩余节点
while (p != NULL) {
r = p->next;
p->next = A->next;
A->next = p;
p = r;
}
while (q != NULL) {
r = q->next;
q->next = A->next;
A->next = q;
q = r;
}
return A; // 返回倒序合并后的链表
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 19、设 A 和 B 是两个单链表(带头结点),其中元素递增有序。设计一个算法从 A 和 B 中的公共元素产生单链表 C,要求不破坏 A、B 的结点。
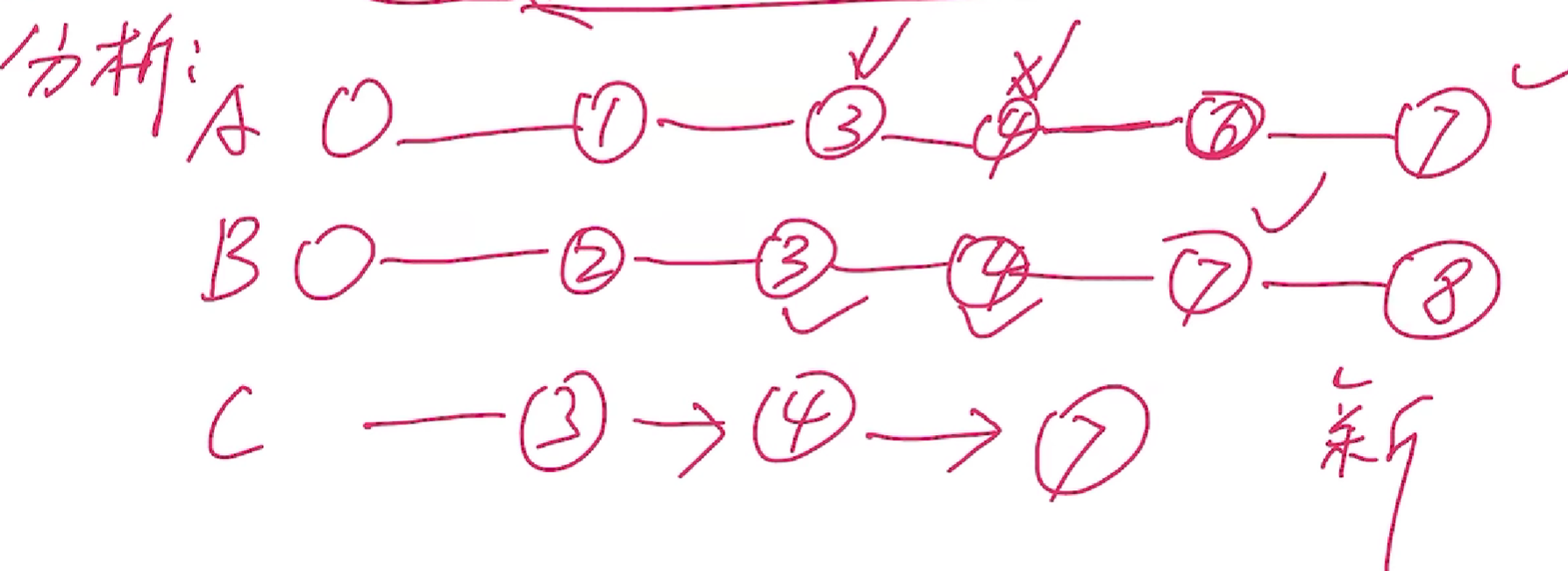
算法思想:两个递增有序,所以两个指针,比较指针元素,那个指针元素小就向后移动,如果相同那么存入C两个指针同时向后移动
LinkList common_data(LinkList A, LinkList B) {
LNode *p = A->next;
LNode *q = B->next;
LinkList C = (LinkList)malloc(sizeof(LNode)); // 初始化链表 C
C->next = NULL;
LNode *r = C; // r 用来跟踪链表 C 的尾部
while (p != NULL && q != NULL) {
if (p->data < q->data) {
p = p->next;
} else if (q->data < p->data) {
q = q->next;
} else {
LNode *s = (LNode *)malloc(sizeof(LNode)); // 动态分配新节点
if (!s) return NULL; // 检查 malloc 是否成功
s->data = p->data; // 公共元素值赋值给新节点
s->next = NULL;
r->next = s; // 插入到链表 C 的尾部
r = s; // 更新尾指针
p = p->next;
q = q->next;
}
}
return C; // 返回包含公共元素的链表 C
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 20、已知两个链表 A 和 B 分别表示两个集合,其元素递增有序排列。编制函数,求 A 和 B 的交集,并存放于 A 链表中。
思路:指针指向 A->next,A->next=NULL 断链,然后公共的尾插入 A 中
void common(LinkList A, LinkList B) {
LNode *p = A->next;
LNode *q = B->next;
A->next = NULL; // 断链,重新建立公共元素的链表
LNode *r = A; // 用于记录链表的尾部
while (p != NULL && q != NULL) {
if (p->data < q->data) {
p = p->next; // p 节点值小,p 向前移动
} else if (q->data < p->data) {
q = q->next; // q 节点值小,q 向前移动
} else {
// 找到相同的元素,将 p 节点放入 A
LNode *temp = p->next; // 保存 p 的下一个节点
r->next = p; // 把 p 接到链表 A 的尾部
r = p; // 更新尾指针
p = temp; // p 移动到下一个节点
q = q->next; // q 移动到下一个节点
}
}
r->next = NULL; // 断开末尾指针
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 21、两个整数序列 A=a1,a2,a3...am 和 B=b1,b2,b3...,bn 已经存入两个单链表中,设计一个算法,判断序列 B 是否是序列 A 的连续子序列。
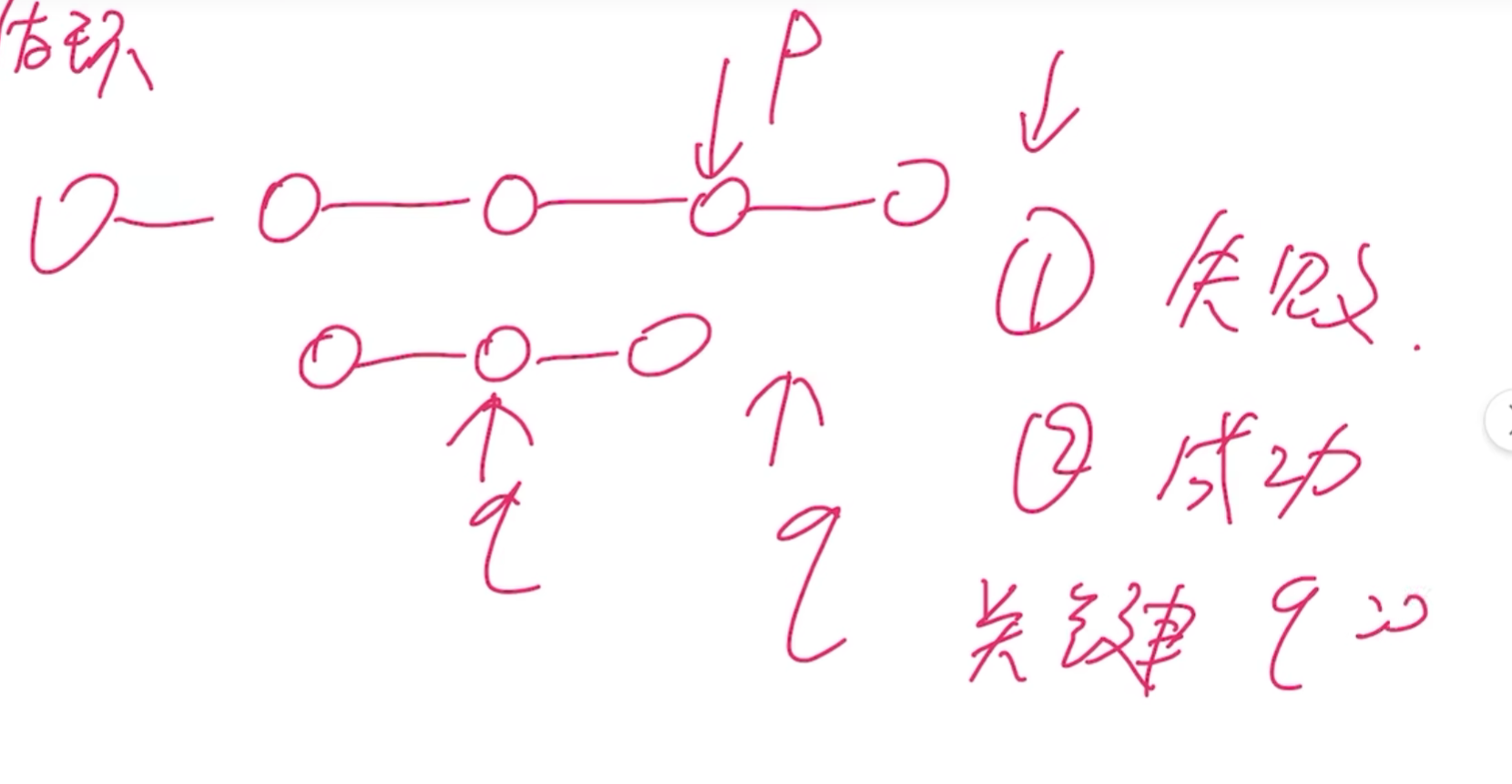 思路:
思路:
bool isSubsequence(LinkList A, LinkList B) {
LNode *p = A->next;
LNode *q = B->next;
// 如果 B 是空链表,B 是 A 的子序列
if (q == NULL) {
return true;
}
// 遍历链表 A
while (p != NULL) {
LNode *temp = p; // 记录当前 p 的位置
q = B->next; // 每次重新从 B 的头开始匹配
// 匹配 A 中一段和 B
while (p != NULL && q != NULL && p->data == q->data) {
p = p->next;
q = q->next;
}
// 如果 B 完全匹配完了,说明 B 是 A 的子序列
if (q == NULL) {
return true;
}
// 否则从 A 的下一个节点继续查找
p = temp->next;
}
// 如果遍历完 A 都没找到匹配,返回 false
return false;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 22、设计一个算法用于判断带头结点的循环双链表是否对称。
typedef struct LNode{
int data;
struct LNode *next;
struct LNode *prev;
}LNode,*DLinkList;
bool isSymmetric(DLinkList L) {
if (L == NULL || L->next == L) {
// 空链表或只有一个元素,认为是对称的
return true;
}
LNode *right = L->next; // 从第一个节点开始
LNode *left = L->prev; // 从最后一个节点开始
// 判断是否对称
while (right != left && left->next != right) {
if (left->data != right->data) {
return false; // 如果数据不相等,返回 false
} else {
left = left->prev; // 向左移动
right = right->next; // 向右移动
}
}
return true; // 完全对称,返回 true
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 22、有两个循环单链表,链表头指针分别为 h1 和 h2,编写一个函数将链表 h2 链接到链表 h1 之后,要求链接后的链表仍保持循环链表的形式。
typedef struct LNode{
int data;
struct LNode *next;
}LNode,*LinkList;
void merge(LinkList h1, LinkList h2) {
if (h1 == NULL || h2 == NULL) {
return; // 如果任意一个链表为空,则直接返回
}
LNode *p = h1->next; // h1 链表的第一个节点
LNode *q = h2->next; // h2 链表的第一个节点
// 找到 h1 的尾节点
LNode *ptail = h1;
while (ptail->next != h1) {
ptail = ptail->next;
}
// 找到 h2 的尾节点
LNode *qtail = h2;
while (qtail->next != h2) {
qtail = qtail->next;
}
// 合并 h1 和 h2
ptail->next = q; // h1 的尾节点指向 h2 的第一个节点
qtail->next = p; // h2 的尾节点指向 h1 的第一个节点
// 删除 h2 的头节点,保持合并后的链表以 h1 为头
free(h2);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 24、设有一个带头节点的的循环单链表,其结点值均为正整数。设计一个算法,反复找出单链表中结点值最小的结点并输出,然后将该结点从中删除,直到单链表为空为止,再删除表头结点。
回顾:试编写带头节点的的单链表 L 中删除一个最小值节点的高效算法(假设最小值节点是唯一的)(day9)
// 删除最小值节点并输出
void deleteMinNode(LinkList L) {
LNode *pre, *minPre, *p, *minP;
while (L->next != L) { // 当链表不为空时
pre = L;
p = L->next;
minP = p; // 假设第一个节点是最小节点
minPre = pre; // 最小节点的前驱节点
// 遍历链表,找到最小值节点
while (p != L) {
if (p->data < minP->data) {
minP = p;
minPre = pre;
}
pre = p;
p = p->next;
}
// 输出最小节点值
printf("Deleted node with value: %d\n", minP->data);
// 删除最小值节点
minPre->next = minP->next;
free(minP);
}
// 链表为空,删除头节点
free(L);
printf("All nodes deleted, including the head node.\n");
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 25

struct LNode{
int data;
int freq;
struct LNode *next;
struct LNode *prev;
}
// Locate(L, x) 函数的实现
struct LNode* Locate(struct LNode* L, int x) {
LNode *p = L->next;
// 找到值为 x 的节点
while(p != NULL && p->data != x) {
p = p->next;
}
// 如果没有找到值为 x 的节点,返回 NULL
if(p == NULL) {
return NULL;
}
// 增加访问频率
p->freq++;
// 从当前位置删除节点 p
if(p->prev != NULL) {
p->prev->next = p->next;
}
if(p->next != NULL) {
p->next->prev = p->prev;
}
// 找到插入位置,根据 freq 排序
LNode *t = p->prev;
while(t != L && t->freq <= p->freq) {
t = t->prev;
}
// 将 p 插入到新位置 t 之后
if(t == L) {
// 插入到头节点之后
p->next = L->next;
if(L->next != NULL) {
L->next->prev = p;
}
L->next = p;
p->prev = L;
} else {
// 插入到 t 之后
p->next = t->next;
if(t->next != NULL) {
t->next->prev = p;
}
t->next = p;
p->prev = t;
}
return p;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 26、寻找单链表倒数第 k 个元素的值
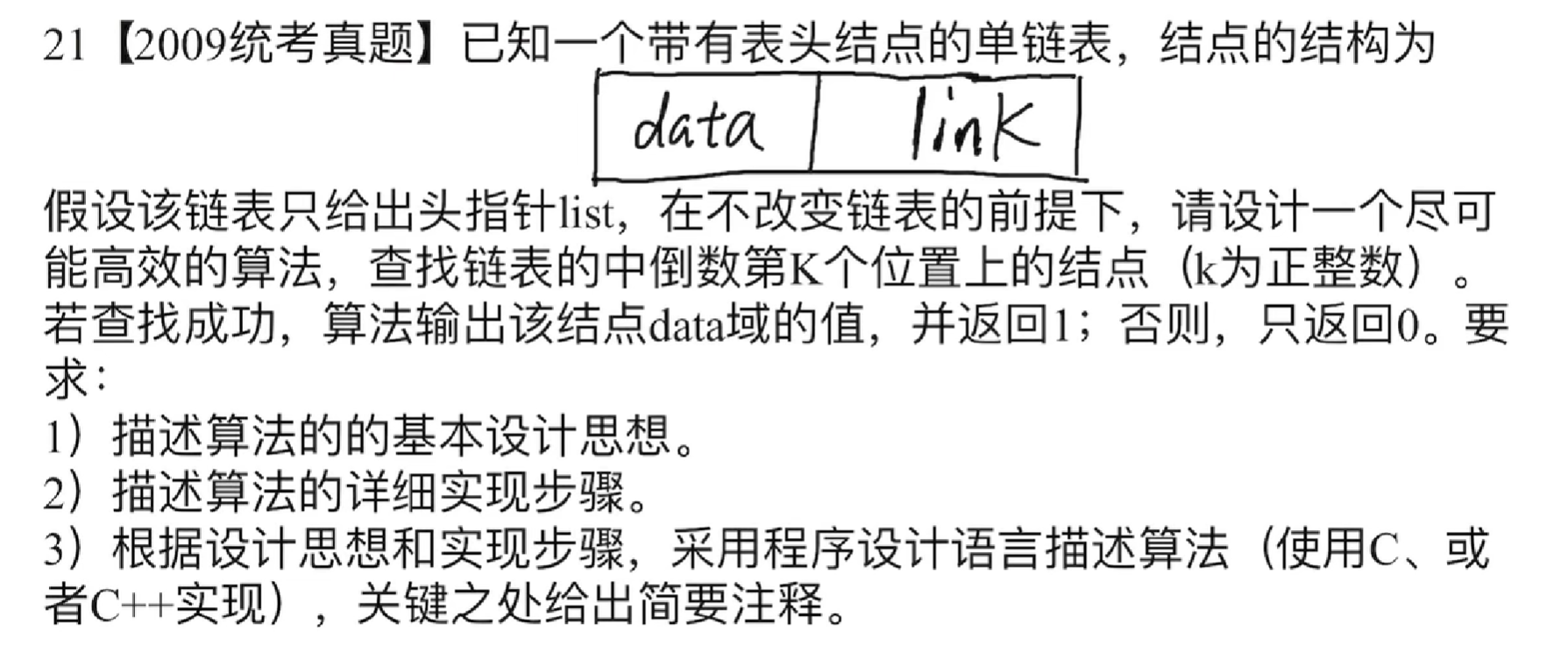
思路:利用快慢指针,快指针先后移动 k 个位置,那么快慢指针一起向后移动,直到快指针指=NULL 后那么慢指针指向的就是倒数第 k 个值
typedef struct LNode{
int data;
struct LNode *link;
}LNode,LinkList;
int search_k(LinkList *L, int k) {
// 快慢指针初始化
LNode *fast = L->link;
LNode *slow = L->link;
// 快指针先走 k 步
for(int i = 0; i < k; i++) {
// 如果 fast 为空,说明链表长度小于 k
if(fast == NULL) {
return -1; // 返回 -1 表示未找到
}
fast = fast->link;
}
// 快慢指针一起走,直到快指针到达链表末尾
while(fast != NULL) {
slow = slow->link;
fast = fast->link;
}
// 返回倒数第 k 个节点的值
return slow->data;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 27、单链表公共后缀,返回后缀起点
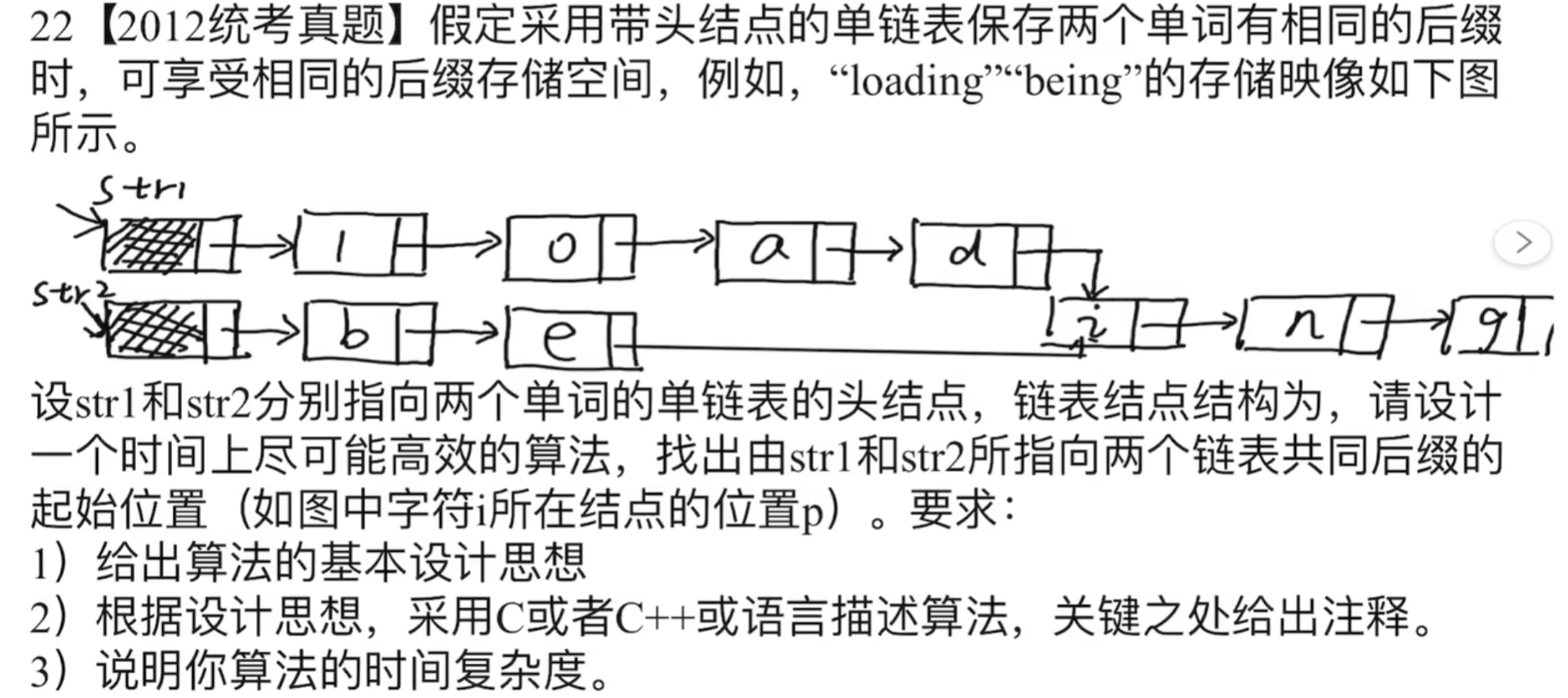
思路:1.获取两个链表长度,长的向后移动到长度相同的位置在开始比较,依次向后移动指针直到第一个相同的结点返回即可
int getlen(LinkList L) {
if(L == NULL || L->next == NULL) {
return 0;
}
LNode *p = L->next;
int len = 0; // 初始化为 0,因为头节点不算在长度中
while(p != NULL) {
len++;
p = p->next;
}
return len;
}
LNode* common_tail(LinkList str1, LinkList str2) {
int len1 = getlen(str1);
int len2 = getlen(str2);
LNode *p = str1->next;
LNode *q = str2->next;
// 让较长的链表先走 |len1 - len2| 步
if(len1 < len2) {
for(int i = 0; i < len2 - len1; i++) {
q = q->next;
}
} else {
for(int i = 0; i < len1 - len2; i++) {
p = p->next;
}
}
// 一起向后遍历,直到找到相同的节点
while(p != NULL && q != NULL) {
if(p == q) { // 比较节点指针,而不是 data
return p; // 找到公共尾部节点
}
p = p->next;
q = q->next;
}
// 没有找到公共尾部节点
return NULL;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 28、绝对值相同的结点只保留一个->利用标记数组
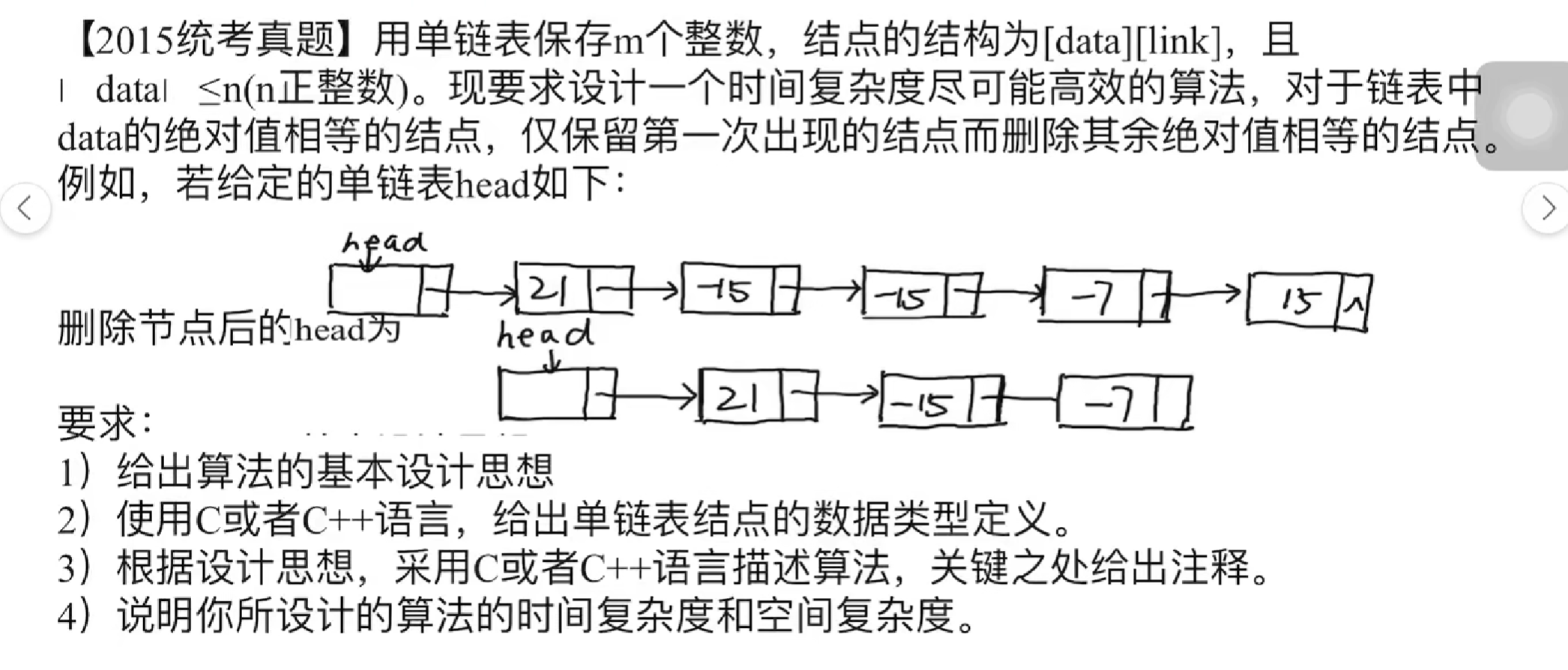
思路:用空间换时间,用标记数组长度为 n+1,都赋值为 0,如果是 0 就可以存入,不是 0 那么就删除
void removeDuplicates(LinkList L, int n) {
bool visited[n+1]; // 这里修正了布尔类型的声明
for(int i = 0; i < n + 1; i++) {
visited[i] = false; // 初始化标记数组
}
LNode *pre = L; // 前驱节点初始化为头节点
LNode *p = L->next; // 当前节点初始化为第一个有效节点
while(p != NULL) {
int data = p->data > 0 ? p->data : -p->data; // 取绝对值
if(visited[data]) {
// 如果当前节点值的绝对值已访问,删除该节点
pre->next = p->next;
free(p); // 释放当前节点内存
p = pre->next; // 移动到下一个节点
} else {
// 否则,标记该值,并继续
visited[data] = true;
pre = p; // 更新前驱节点
p = p->next; // 移动到下一个节点
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 29、

思路:快慢指针找到中间结点,后半部分逆置(头插法),然后逐个插入前面要求位置
找到链表的中点:通过双指针(快慢指针)找到链表的中点。
反转链表的后半部分:从中点开始,反转链表的后半部分。
交替合并两部分链表:将前半部分和反转后的后半部分交替合并。
void rearrangeList(LinkList L) {
// 快慢指针找到链表的中间位置
LNode *fast = L, *slow = L;
while (fast->next != NULL && fast->next->next != NULL) {
fast = fast->next->next;
slow = slow->next;
}
// 反转链表的后半部分
LNode *p = slow->next, *temp;
slow->next = NULL; // 前后部分分开
LNode *rear = NULL; // 初始化为NULL,表示反转后的链表为空
// 反转后半部分链表
while (p != NULL) {
temp = p->next;
p->next = rear;
rear = p;
p = temp;
}
// 合并前半部分和反转后的后半部分
LNode *ptemp, *qtemp;
LNode *q = rear; // q指向反转后的链表
p = L->next; // p指向前半部分链表
while (p != NULL && q != NULL) {
ptemp = p->next;
qtemp = q->next;
q->next = p->next; // 将q插入p之后
p->next = q;
p = ptemp;
q = qtemp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 二叉树
# 31、 巳知一棵二叉树按顺序存储结构进行存储,设计一个算法,求编号分别为 i 和 i 的两个节点的最近公共祖先结点的值。
int findLCA(int i, int j) {
// 如果两个节点编号相同,直接返回该节点
if (i == j) {
return i;
}
// 不断将 i 和 j 向上移动到父节点,直到它们相等
while (i != j) {
if (i > j) {
i = i / 2; // i 移动到父节点
} else {
j = j / 2; // j 移动到父节点
}
}
// 此时 i == j,即最近公共祖先
return i;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 32、二叉树遍历
// 前序遍历递归实现
void preOrder(BiTree T){
if(T!=NULL){
visit(T);
preOrder(T->left);
perOrder(T->right);
}
}
// 中序遍历递归实现
void inOrder(BiTree T){
if(T!=NULL){
inOrder(T->left);
visit(T);
inOrder(T->right);
}
}
// 后序遍历递归实现
void postOrder(BiTree T){
if(T!=NULL){
postOrder(T->left);
postOrder(T->right);
visit(T);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 33、二叉树非递归遍历
//先序非递归遍历二叉树 (背诵法:先序非递归遍历:非空打印推入往左走,空了弹出往右走)
void nonPre(BiTree T){
InitStack(S);
BiTree root = T;
while(root!=NULL||!isEmpty(S)){
if(root != NULL){
printf("%d",root->data)
push(S,root);
root = root->left;
}else{
pop(S,root);
root = root->right;
}
}
}
//中序非递归遍历 (背诵法:入栈向左一直走,出栈、访问、右子树)
void nonIn(BiTree T){
InitStack(S);
BiTree root = T;
while(root || !isEmpty(S)){
if(root !=NULL){
push(S,root);
root = root->left;
}else{
pop(S,root);
printf("%d",root->data);
root = root->right;
}
}
}
// 后序非递归 (向左一直走,为空查看有右子树且没访问想右走,否则弹出访问标记访问且设为NULL)
void nonPost(BiTree T) {
BiTree root = T;
BiTree temp;
BiTree tag = NULL; // 用于标记已访问过右子树的节点
// int top = -1;
// BiTree *S[10]; 手写版本不过要指定长度
initStack(S);
while(root||!isEmpty(S)){
if(root != NULL){
// S[++top] = root;
push(S,root);
root=root->left;
}else{
// temp = S[top];
temp = getTop(S);
// 如果当前节点有右子树,并且右子树没有被访问过
if(temp->right && temp->right != tag){
root = temp->right;
}else{
//temp = S[top--];
temp = pop(S);
printf("%d",temp->data);
tag = temp;
root = NULL; // 防止继续访问左子树
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
# 35、树层次遍历
void level(BiTree T){
// int front=0,reaar =0;
// BTNode *que[10];
InitQueue(Q);
BiTree p;
if(p!=NULL){
// que[front++] = T;
EnQueue(Q,T);
while(!isEmpty(Q)){
// p = que[rear++];
DeQueue(Q,p);
printf("%d",p->data);
if(p->left!=NULL){
// que[font++] = p->left;
EnQueue(Q,p->left);
}
if(p->right!=NULL){
EnQueue(Q,p->right);
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 36、试给出二叉树的至下而上、从右到左的层次遍历算法
思路:层次遍历是从上至下,从左至右,所以添加入栈,逆序即可
void level(BiTree T){
InitQueue(Q);
InitStack(S);
EnQueue(Q,T);
BiTree p;
while(!isEmpty(Q)){
DeQueue(Q,p);
push(S,p); //入栈
if(p->left !=NULL){
EnQueue(Q,p->left);
}
if(p->right!=NULL){
EnQueue(Q,p->right);
}
}
while(!isEmpty(S)){ //将栈中元素打印出即从下至上,从右至左
pop(S,p);
printf("%d",p->data);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 37、假设二叉树采用二叉链表存储结构,设计一个算法求二叉树的高度(递归和非递归)
递归算法思想:递归求左右子树高度,取较大的加1
int treeHeight(BiTree T){
if(T == NULL){
return 0;
}
int left = treeHight(T->left);
int right = treeHith(T->right);
return (left>right?left:right)+1; // 返回最大高度加1
}
2
3
4
5
6
7
8
9
10
11
12
非递归算法思路:采用层次遍历,变量level记录二叉树层次,指针last指向最右结点
如何指向每一层最后结点?
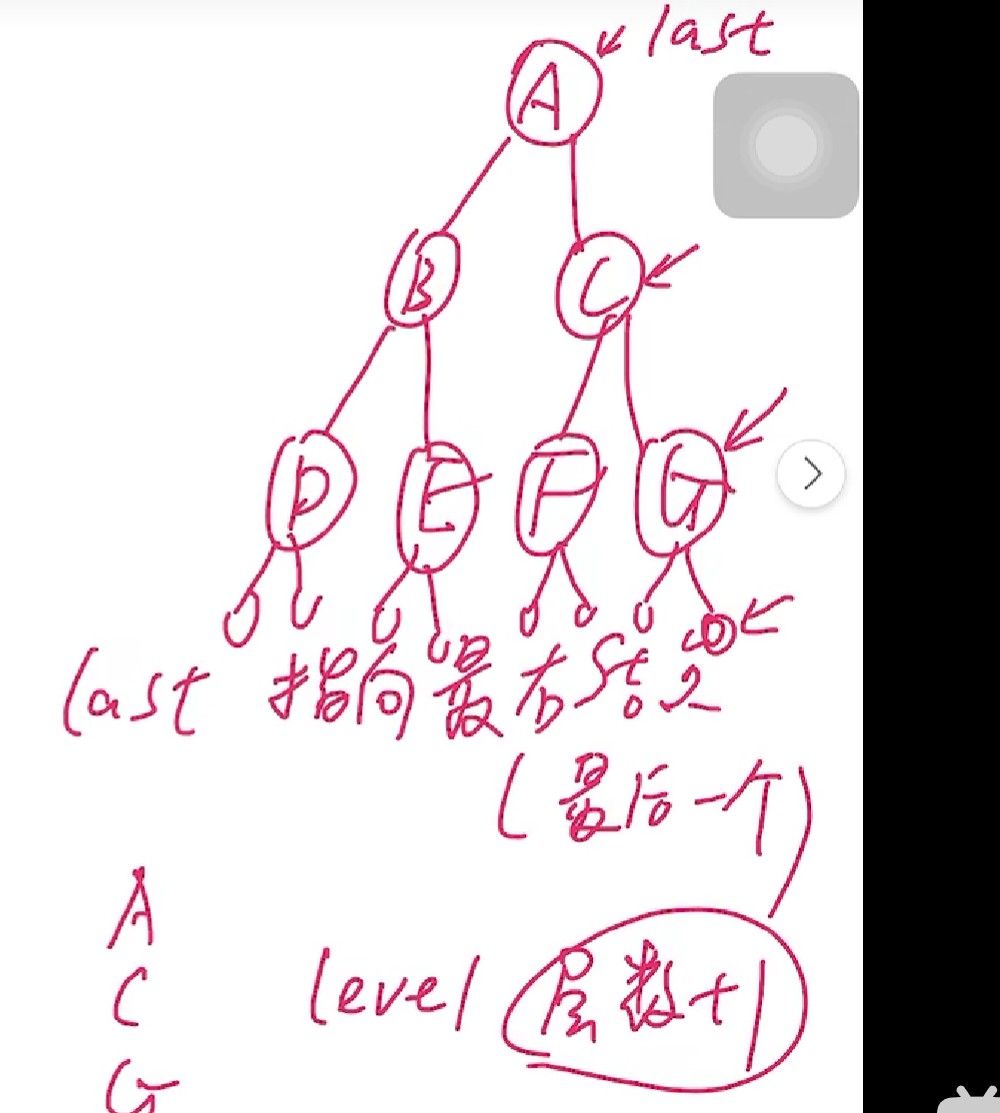
void Btdepth(BiTree T){
if (T == NULL) { // 如果树为空
return 0;
}
int front = -1,rear = -1;
int last = 0,level = 0;
BiTree Q[maxsize];
// 将根节点入队
Q[++rear] = T;
last = rear;
BiTree p;
while(front <rear){
p = Q[++front]; // 出队操作
// 将左子节点入队
if (p->left != NULL) {
Q[++rear] = p->left;
}
// 将右子节点入队
if (p->right != NULL) {
Q[++rear] = p->right;
}
// 如果当前层的最后一个节点已经出队,增加层数
if (front == last) {
level++;
last = rear; // 更新下一层的最后一个节点
}
}
return level;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 38、设树B是一棵采用链式结构存储的二叉树,编写一个把树中所有结点的左右子树交换的函数。【中国科学院大学2015】
思路:先交换根的左右结点,再递归左右一样的操作
void swap(BiTree T){
if(T!=NULL){
BiTree p = T->left;
T->left = T->right;
T->right = p;
swap(T->left);
swap(T->right);
}
}
2
3
4
5
6
7
8
9
10
11
# 39、假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支(度为2)结点个数。【哈尔滨工业大学】
思路:如果是空结点:0、如果是双分支结点+1、单只结点继续递归
int doubleCount(BiTree T){
if(T==NULL){
return 0;
}else if(T->left && T->right){
return doubleCount(T->left) + doubleCount(T->right) +1;
}else{
return doubleCount(T->left) + doubleCount(T->right);
}
}
2
3
4
5
6
7
8
9
10
11
# 40、计算二叉树所有结点个数
int count(BiTree T){
if(T==NULL){
return 0;
}else{
count(T->left) + count(T->right) +1;
}
}
2
3
4
5
6
7
8
9
# 41、假设二叉树采用二叉链存储结构存储,设计一个算法,求先序遍历序列中第K(1≤K≤二叉树中结点个数)个结点的值。
// 全局计数器
int count = 0;
//递归先序遍历
int preOrder(BiTree T,int k){
if(T!=NULL){
return NULL;
}
// 如果当前节点是第 K 个节点,返回该节点的值
if(count == k){
return T->data;
}
int leftCount = preOrder(T->left,k);
if(leftCount != NULL){
return leftCount;
}
return preOrder(T->right,k);
}
//非递归先序遍历求第k个
int preOrder(BiTree T,int k){
if(T==NULL){
return NULL;
}
BiTNode *cur = T;
BiTNode *stack[MAXSIZE];
int top = -1;
int count = 0;
stack[++top] = T;
while(cur != NULL || top != -1){
if(cur!=NULL){
count++;
if(count == k){
return cur->data;
}
stack[++top] = cur->left;
cur = cur->left;
}else{
cur = stack[top--];
cur = cur->right;
}
}
return count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# 42、计算二叉树中所有的叶子结点个数
//递归实现
int count =0;
void preOrder(BiTree T){
if(T!=NULL){
if(T->left != NULL && T->right !=NULL){
count++;
}
preOrder(T->left);
preOrder(T->right);
}
}
//非递归 后序
void postOrder(BiTree T){
BiTNode *stack[MAXSIZE];
int top=-1;
int count = 0;
BiNode *p = T;
while(p!=NULL || top != -1){
if(p!=NULL){
stack[++top];
p = p->left;
}else{
p = stack[top]
if(p->right !=NUL){
p = p->right;
}else{
p = stack[top--];
count++;
printf("%d ",p->data);
tag = p;
p = NULL;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 43、查找二叉树中data域等于key的结点是否存在,若存在,将q指向它,否则g为空
BiTNode* findKey(BiTree T, int key) {
if (T == NULL) {
return NULL; // 如果当前节点为空,返回空指针
}
if (T->data == key) {
return T; // 如果找到目标节点,返回该节点指针
}
// 先在左子树查找
BiTNode* leftResult = findKey(T->left, key);
if (leftResult != NULL) {
return leftResult; // 如果在左子树找到,直接返回
}
// 再在右子树查找
return findKey(T->right, key);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 44、利用结点的右孩子指针将一个二叉树的叶子结点从左向右链接成一个单链表(head指向第一个tail指向最后一个)
// 全局指针用于链表的头和尾
BiTNode* head = NULL;
BiTNode* tail = NULL;
void linkLeaves(BiTree T){
if(T == NULL){
return NULL;
}
if(T->left !=NULL && T->right !=NULL){
if(head==NULL){
head = T;
tail = T;
}else{
tail->next = T;
tail = T;
}
tail->next = NULL;
}
linkLeaves(T->left);
linkLeaves(T->right;)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 45、若二叉树采用链式存储结构,设求出指定结点在给定二叉树排序树的层次
思路:
如果目标值小于当前节点的值,递归进入左子树;
如果目标值大于当前节点的值,递归进入右子树;
如果找到节点,则返回当前的层次值。
int findLevel(BiTree root, int key, int level) {
if (root == NULL) {
return 0; // 节点不存在,返回 0 表示没有找到
}
if (root->data == key) {
return level; // 找到指定节点,返回当前层次
}
// 如果目标节点的值小于当前节点,进入左子树
if (key < root->data) {
return findLevel(root->left, key, level + 1);
} else { // 如果目标节点的值大于当前节点,进入右子树
return findLevel(root->right, key, level + 1);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 46、求二叉树WPL

int calculateWPL(BiTree T,int deep){
if(T== NULL){
return 0;
}
if(T->left != NULL && T->right !=NULL){
return T->data * deep;
}
//递归
int leftWPL = calculateWPL(T->left,deep+1);
int rightWPL = calculateWPL(T->right,deep+1);
//求和
return leftWPL+rightWPL;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 47、二叉树转换为中缀表达式

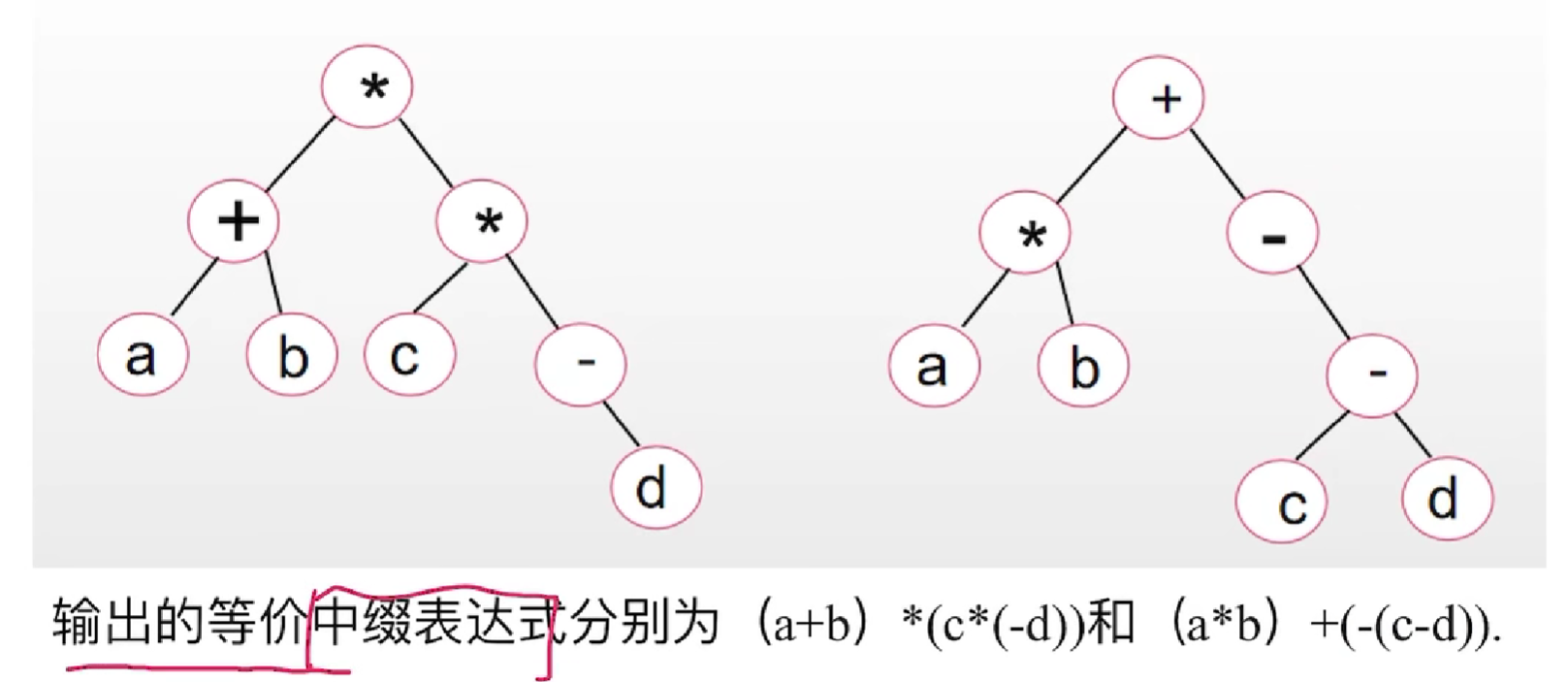
观察:根节点,叶子结点不加括号,其他结点要加括号(中序访问左子树之前加,右子树之后加)
// 递归生成中缀表达式
void InOrderFun(BiTree* T, int deep) {
if (T == NULL) {
return;
}
// 判断是否为叶子节点
if (T->left == NULL && T->right == NULL) {
printf("%s", T->data); // 叶子节点直接输出
} else {
if (deep > 1) printf("("); // 根据深度决定是否输出括号
InOrderFun(T->left, deep + 1);
printf("%s", T->data); // 输出当前节点
InOrderFun(T->right, deep + 1);
if (deep > 1) printf(")"); // 根据深度决定是否输出括号
}
}
//中缀表达式为: ((a+b)*((c+(-d))))
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 48、假设二叉树采用二叉链表结构存储,设计一个算法,求二叉树中值为x的层号。
int levelFor_K(BiTree T, int deep, int k) {
if (T == NULL) {
return 0; // 空节点返回0,表示没有找到
}
if (T->data == k) {
return deep; // 找到节点,返回当前深度
}
// 递归查找左子树
int left_K = levelFor_K(T->left, deep + 1, k);
if (left_K != 0) {
return left_K; // 如果在左子树找到,返回其深度
}
// 递归查找右子树
return levelFor_K(T->right, deep + 1, k);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 49、请设计一个算法,增加一个指向双亲结点的parent指针,并给指向指针赋值,并输出所有结点到根结点的路径
void setParent(BiTree T,BiTNode *parent){
if(T==NULL){
return ;
}
T->parent = parent;
setParent(T->left,T);
setParent(T->right,T);
}
setParent(T,NULL);
2
3
4
5
6
7
8
9
10
11
12
13
# 50、已知一棵二叉树链式存储,请设计一个算法,输出根结点到每个叶子结点的路径【哈尔滨工业大学】
思路:
递归遍历树,并在遍历过程中记录从根到当前结点的路径。
如果当前结点是叶子结点,输出路径。
int top=-1;
BiTNode *stack[MAXSIZE];
void printPathsRecur(BiTree T){
if(T == NULL) return ;
stack[++top] = p;
if(T->left == NULL && T->right == NULL){ //判断是否为结点点
//是叶结点,将栈中数据打印输出
for(int i=0;i<=top;i++){
printf("%c",stack[i].data);
}
}else{
printPathsRecur(T->left);
printPathsRecur(T->right);
}
top--;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 图
图的数据结构:邻接表、邻接矩阵
# 邻接表:
// 邻接表中的边结点结构体
typedef struct ANode {
int adjvex; // 边所指向的结点的编号(顶点位置)
struct ANode *nextarc; // 指向下一个边结点的指针,用于链接其他边
} ANode, *Node; // ANode是边结点结构体的别名,Node是指向ANode的指针类型
// 邻接表中的顶点结点结构体
typedef struct {
int data; // 顶点的数据(例如顶点的标识)
ANode *firstarc; // 指向该顶点的第一条边(邻接点)的指针
} Vnode;
// 图结构体,使用邻接表表示
typedef struct {
int numver, numedg; // numver表示顶点数,numedg表示边数
Vnode adjList[maxsize]; // 邻接表数组,存储图中所有顶点和它们的边
} Graph;
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 邻接表的遍历
// 邻接表广度优先
void BFS(Graph *G, int startVertex) { // 输入图的指针和开始遍历的顶点
int visit[maxsize] = {0}; // 访问标记数组,用来记录顶点是否被访问过,0表示未访问,1表示已访问
int que[maxsize]; // 队列用于存储待访问的顶点
int front = 0, rear = 0;
visit[startVertex] = 1; // 标记起始顶点为已访问
que[++rear] = startVertex; // 将起始顶点入队
while (front != rear) { // 当队列不为空时,循环继续
int currentV = que[++front]; // 从队列中取出队首顶点
printf("%d ", currentV);
Node p = G->adjList[currentV].firstarc; // 获取当前顶点的邻接表的第一个邻接顶点
while (p != NULL) { //
if (visit[p->adjvex] == 0) {
visit[p->adjvex] = 1;
que[++rear] = p->adjvex; // 将该邻接顶点入队
}
p = p->nextarc; // 移动到下一个邻接顶点
}
}
}
// 邻接表深度优先
void DFS(Graph *G,int startV,int visit[]){
printf("%d ",startV);
visit[startV] = 1;
Node p = G->adjList[startV].firstarc;
while(p!=NULL){
if(visit[p->adjvex]==0){
DFS(G,p->adjvex,visit);
}
p=p->nextarc;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 邻接矩阵结构体:
// 邻接矩阵结构体
typedef struct {
int numver, numedg; // numver表示顶点数,numedg表示边数
int verticle[maxsize]; // 存储顶点的数组
int Edge[maxsize][maxsize]; // 邻接矩阵,存储图中顶点之间的边(0表示无边,非0表示有边)
} mGraph;
2
3
4
5
6
7
# 排序大关
# 冒泡排序
//冒泡排序
void bubbleSort(int arr[], int n) {
for(int i=0;i<n-1;i++){
for(int j = 0;j<n-i-1;j++){
if(arr[j]>arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# 选择排序
//选择排序,每次选择一个最小的
void selectionSort(int arr[], int n) {
for(int i=0;i<n;i++){
int minIndex = i;
for(int j = i+1;j<n;j++){
if(arr[j]<arr[minIndex]){
minIndex = j;
}
}
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 插入排序
//直接插入排序
void insertionSort(int arr[], int n) {
for(int i=1;i<n;i++){
int key = arr[i];
int j=i-1;
while(j>=0&&arr[j]>key){
arr[j+1] = arr[j--];
}
arr[j+1] = key;
}
}
2
3
4
5
6
7
8
9
10
11
12
# 折半插入排序
// 二分查找,返回插入位置
int binarySearch(int arr[], int item, int low, int high) {
while(low<=high){
int mid = (low+high)/2;
if(item == arr[mid]){
return mid+1;
}else if(item < arr[mid]){
high=mid-1;
}else{
low=mid+1;
}
}
return low;
}
void binaryInsertionSort(int arr[], int n) {
for(int i=1;i<n;i++){
int key = arr[i];
int j = i-1;
int pos = binarySearch(arr,key,0,j);
while(j>=pos){
arr[j+1] = arr[j--];
}
arr[pos] = key;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 快速排序
int partition(int arr[], int low, int high) {
int pivot = arr[low]; // 选择第一个元素作为基准
// 开始分区操作
while (low < high) {
while (low < high && arr[high] > pivot) {// 从右侧找到一个小于基准的元素
high--;
}
arr[low] = arr[high]; // 将小于基准的元素放到左侧
while (low < high && arr[low] < pivot) { // 从左侧找到一个大于基准的元素
low++;
}
arr[high] = arr[low]; // 将大于基准的元素放到右侧
}
arr[low] = pivot; // 将基准元素放到正确的位置
return low; // 返回基准元素的最终位置
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
int mid = partition(arr, low, high); // 对数组进行分区
quickSort(arr, low, mid - 1); // 递归排序左侧子数组
quickSort(arr, mid + 1, high); // 递归排序右侧子数组
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 二路归并排序
#include <stdio.h>
// 合并两个子数组:arr[left..mid] 和 arr[mid+1..right]
void merge(int arr[], int left, int mid, int right) {
// 计算左右子数组的长度
int n1 = mid - left + 1; // 左子数组的长度
int n2 = right - mid; // 右子数组的长度
// 创建两个临时数组来存储左右子数组的元素
int L[n1], R[n2];
// 将数据复制到左子数组 L 和右子数组 R 中
for (int i = 0; i < n1; i++) {
L[i] = arr[left + i];
}
for (int j = 0; j < n2; j++) {
R[j] = arr[mid + 1 + j];
}
// 初始化索引 i 和 j 用于遍历 L 和 R,以及 k 用于遍历合并后的数组 arr
int i = 0, j = 0, k = left;
// 合并 L 和 R 数组中的元素,按升序排列
while (i < n1 && j < n2) {
if (L[i] <= R[j]) { // 若 L[i] 小于等于 R[j],将 L[i] 插入 arr
arr[k++] = L[i++];
} else { // 若 R[j] 小于 L[i],将 R[j] 插入 arr
arr[k++] = R[j++];
}
}
// 将剩余的 L 数组元素(如果有)复制到 arr
while (i < n1) {
arr[k++] = L[i++];
}
// 将剩余的 R 数组元素(如果有)复制到 arr
while (j < n2) {
arr[k++] = R[j++];
}
}
// 递归实现归并排序
void mergeSort(int arr[], int left, int right) {
if (left < right) { // 基础条件:当 left >= right 时,数组已排序
int mid = (left + right) / 2; // 找到数组的中间点
// 递归排序左半部分
mergeSort(arr, left, mid);
// 递归排序右半部分
mergeSort(arr, mid + 1, right);
// 合并已排序的左右部分
merge(arr, left, mid, right);
}
}
int main() {
int arr[] = {12, 11, 13, 5, 6, 7};
int arr_size = sizeof(arr) / sizeof(arr[0]);
printf("给定的数组: ");
printArray(arr, arr_size);
// 归并排序
mergeSort(arr, 0, arr_size - 1);
printf("排序后的数组: ");
printArray(arr, arr_size);
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# 查找
# 二分查找
//非递归二分查找
int binarySearch(int arr[], int size, int target) {
int low = 0,high = size-1,mid;
while(low<=high){
mid = (low+high)/2;
if(arr[mid] = target){
return mid+1;
}else if(arr[mid] > target){
high = mid-1;
}else{
low = mid +1;
}
}
}
// 递归二分查找函数
int binarySearchRecursive(int arr[], int low, int high, int target) {
if(low>high){
return -1;
}
int mid = (low+high)/2;
if(arr[mid] == target){
return mid+1;
}else if(arr[mid]>target){
return binarySearchRecursive(arr,low,mid-1,target);
}else{
return binarySearchRecursive(arr,mid+1,high,target);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
